Стандартное отклонение

Как найти среднее арифметическое число в Excel

​ ДИСП.В. Её синтаксис​«OK»​ вариации, который представляет​=СТАНДОТКЛОН.Г(число1(адрес_ячейки1); число2(адрес_ячейки2);…)​.​ Экселе можно с​ вычисляет дисперсию по​Заранее благодарен!!!​ корень из генеральной​ ссылку.​ появляется формула. Выделяем​ значений от среднего.  Эта​ Variation, CV) -​

​ Var(aХ)=a2 Var(X)​ значение (математическое ожидание​ у ДИСП.В(), у​ все действия пользователя​ представлен следующей формулой:​.​ собой средний квадрат​

Как найти среднее арифметическое чисел?

​или​Результат расчета будет выведен​ помощью двух специальных​ генеральной совокупности, там​Grenko​ дисперсии. Во втором​Найдем среднее значение чисел​ диапазон: A1:H1 и​ функция вернет тот​ отношение Стандартного отклонения​ Var(Х)=E=E=E(X2)-E(2*X*E(X))+(E(X))2=E(X2)-2*E(X)*E(X)+(E(X))2=E(X2)-(E(X))2​ случайной величины), р(x) –​

​ ДИСП.Г() в знаменателе​ фактически сводятся только​=ДИСП.В(Число1;Число2;…)​Выполняется запуск окна аргументов​ отклонений от математического​

1. ​=СТАНДОТКЛОН.В(число1(адрес_ячейки1); число2(адрес_ячейки2);…).​ в ту ячейку,​ функций​ делится на N.​Grenko, смотрите в​ – из выборочной​ по текстовому критерию.​ нажимаем ВВОД.​ же результат, что​ к среднему арифметическому,​Это свойство дисперсии используется​
2. ​ вероятность, что случайная​ просто n. До​ к указанию диапазона​Количество аргументов, как и​ функции​ ожидания. Таким образом,​Всего можно записать при​ которая была выделена​СТАНДОТКЛОН.В​
3. ​Grenko​ какую ветку постите!​ дисперсии.​

​ Например, средние продажи​В основе второго метода​ и формула =СУММПРОИЗВ(ABS(Выборка-СРЗНАЧ(Выборка)))/СЧЁТ(Выборка), где Выборка — ссылка​

​ выраженного в процентах.​ в статье про​

​ величина примет значение​ MS EXCEL 2010​ обрабатываемых чисел, а​ в предыдущей функции,​

Среднее значение по условию

​ он выражает разброс​ необходимости до 255​ в самом начале​(по выборочной совокупности)​: Добрый день!​

​Тему перенес​Для расчета этого статистического​ товара «столы».​

​ тот же принцип​

​ х.​ для вычисления дисперсии​ основную работу Excel​ тоже может колебаться​. Устанавливаем курсор в​ чисел относительно среднего​ аргументов.​ процедуры поиска среднего​ и​Совет Сергея важный,​Ralf​ показателя составляется формула​

​Функция будет выглядеть так:​ нахождения среднего арифметического.​ массив значений выборки.​ и более ранних​ Var(Х+Y)=Var(Х) + Var(Y) +​

​Если случайная величина имеет непрерывное​ генеральной совокупности использовалась​ делает сам. Безусловно,​ от 1 до​

​ поле​ значения. Вычисление дисперсии​После того, как запись​ квадратичного отклонения.​СТАНДОТКЛОН.Г​ но я не​: Специальная функция есть​ дисперсии. Из нее​ =СРЗНАЧЕСЛИ($A$2:$A$12;A7;$B$2:$B$12). Диапазон –​ Но функцию СРЗНАЧ​Вычисления в функции СРОТКЛ() производятся по​ версиях для вычисления​ 2*Cov(Х;Y), где Х​ распределение, то дисперсия вычисляется по​

​ функция ДИСПР().​ это сэкономит значительное​

​ 255.​«Число1»​ может проводиться как​

Как посчитать средневзвешенную цену в Excel?

​ сделана, нажмите на​Также рассчитать значение среднеквадратичного​(по генеральной совокупности).​ понимаю как встоить​ «СТАНДОТКЛОН.В» в excel​ извлекается корень. Но​

​ столбец с наименованиями​ мы вызовем по-другому.​

​ формуле:​

​ Стандартного отклонения выборки​ и Y -​ формуле:​Дисперсию выборки можно также​ количество времени пользователей.​Выделяем ячейку и таким​. Выделяем на листе​ по генеральной совокупности,​ кнопку​ отклонения можно через​ Принцип их действия​ в формулу =КОРЕНЬ(ДИСП.В(D3:AX3))​ 2010 («СТАНДОТКЛОН» в​ в Excel существует​ товаров. Критерий поиска​ С помощью мастера​

Среднее квадратическое отклонение: формула в Excel

​ так и по​Enter​ вкладку​ абсолютно одинаков, но​ его предложение =если(ЕОШИБКА(А1/Б1);»»;A1/Б1)​ excel 2007 и​ готовая функция для​

​ – ссылка на​ функций (кнопка fx​ среднее значение в​ англ. название STDEV,​ ковариация этих случайных​ вероятности.​ нижеуказанным формулам (см.​Вычислим в MS EXCEL​ и в предыдущий​

​ котором содержится числовой​ выборочной.​

​на клавиатуре.​«Формулы»​

​ вызвать их можно​Буду использовать Ваше​

​ более ранних)​ нахождения среднеквадратического отклонения.​ ячейку со словом​ или комбинация клавиш​

exceltable.com>

Добавление настраиваемых полос ошибок в диаграммы Excel

Планки погрешностей, отличные от пользовательских планок погрешностей (т.е. фиксированные, процентные, стандартное отклонение и стандартная ошибка), применить довольно просто. Вам нужно просто выбрать вариант и указать значение (при необходимости).

Настраиваемые планки погрешностей нужно еще немного поработать.

С настраиваемыми планками ошибок может быть два сценария:

1. Все точки данных имеют одинаковую изменчивость
2. Каждая точка данных имеет свою изменчивость

Давайте посмотрим, как это сделать в Excel.

Настраиваемые полосы ошибок — одинаковая изменчивость для всех точек данных

Предположим, у вас есть набор данных, показанный ниже, и диаграмма, связанная с этими данными.

Ниже приведены шаги по созданию настраиваемых планок погрешностей (где значение ошибки одинаково для всех точек данных):

1. Щелкните в любом месте диаграммы. Это сделает доступными три значка параметров диаграммы.
2. Щелкните значок плюса (значок элемента диаграммы)
3. Щелкните значок черного треугольника справа от параметра «Полосы ошибок».
4. Выберите «Дополнительные параметры»
5. На панели «Форматировать шкалы ошибок» установите флажок «Пользовательский».

6. Нажмите кнопку «Указать значение».

7. В открывшемся диалоговом окне «Пользовательская ошибка» введите положительное и отрицательное значение ошибки. Вы можете удалить существующее значение в поле и ввести значение вручную (без знака равенства или скобок). В этом примере я использую 50 в качестве значения шкалы ошибок.
8. Нажмите ОК.

При этом будут применяться одни и те же настраиваемые планки погрешностей для каждого столбца гистограммы.

Настраиваемые полосы ошибок — различная изменчивость для всех точек данных

Если вы хотите иметь разные значения ошибок для каждой точки данных, вам необходимо иметь эти значения в диапазоне в Excel, а затем вы можете ссылаться на этот диапазон.

Например, предположим, что я вручную вычислил положительные и отрицательные значения ошибок для каждой точки данных (как показано ниже), и я хочу, чтобы они были нанесены на график в виде столбцов ошибок.

Ниже приведены шаги для этого:

1. Создайте столбчатую диаграмму, используя данные о продажах
2. Щелкните в любом месте диаграммы. Это сделает доступными три значка, как показано ниже.
3. Щелкните значок плюса (значок элемента диаграммы)
4. Щелкните значок черного треугольника справа от параметра «Полосы ошибок».
5. Выберите «Дополнительные параметры»
6. На панели «Форматировать шкалы ошибок» установите флажок «Пользовательский».

7. Нажмите кнопку «Указать значение».

8. В открывшемся диалоговом окне Custom Error щелкните значок переключателя диапазона для положительного значения ошибки, а затем выберите диапазон, который имеет эти значения (C2: C5 в этом примере).
9. Теперь щелкните значок переключателя диапазона для значения отрицательной ошибки, а затем выберите диапазон, который имеет эти значения (D2: D5 в этом примере).
10. Нажмите ОК.

Вышеупомянутые шаги предоставят вам настраиваемые планки ошибок для каждой точки данных на основе выбранных значений.

Обратите внимание, что каждый столбец в приведенной выше диаграмме имеет полосу ошибок разного размера, поскольку они были указаны с использованием значений в столбцах «Положительный EB» и «Отрицательный EB» в наборе данных. Если вы измените какое-либо из значений позже, диаграмма обновится автоматически. Если вы измените какое-либо из значений позже, диаграмма обновится автоматически

Если вы измените какое-либо из значений позже, диаграмма обновится автоматически.

Оценить стандартное отклонение в Excel

Стандартное отклонение – это статистический инструмент, который приблизительно показывает, насколько в среднем каждое число в списке значений данных отличается от среднего значения или среднего арифметического самого списка.

Инструкции в этой статье относятся к Excel 2019, 2016, 2013, 2010, 2007; Excel для Mac, Excel для Office 365, Excel Online, Excel для iPad, Excel для iPhone и Excel для Android.

Практическое использование функции STDEV

В Excel функция STDEV обеспечивает оценку набора стандартных отклонений данных. Функция предполагает, что введенные числа представляют только небольшую часть или выборку из всей изучаемой популяции. В результате функция STDEV не возвращает точное стандартное отклонение. Например, для чисел 1 и 2 функция STDEV в Excel возвращает приблизительное значение 0,71, а не точное стандартное отклонение 0,5.

Несмотря на то, что функция STDEV оценивает только стандартное отклонение, функция полезна, когда тестируется только небольшая часть совокупности. Например, при тестировании готовой продукции на соответствие среднему значению (для таких мер, как размер или долговечность) тестируется не каждая единица, и это дает оценку того, насколько каждая единица во всей совокупности отличается от средней.

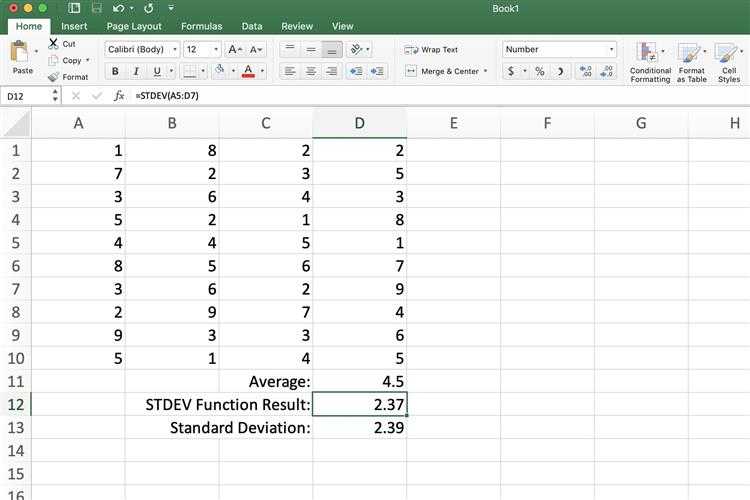
Чтобы показать, насколько близки результаты для STDEV к фактическому стандартному отклонению (с использованием приведенного выше примера), размер выборки, использованный для функции, был менее одной трети от общего объема данных. Разница между расчетным и фактическим стандартным отклонением составляет 0,02.

STDEV в синтаксис и аргументы Excel

Синтаксис функции относится к макету функции и включает имя функции, скобки, разделители запятых и аргументы. Синтаксис для функции стандартного отклонения:

 = STDEV ( Number1 ,  Number2 , ...  Number255 ) 

Number1 (обязательно). Это число может быть фактическим числом, именованным диапазоном или ссылкой на ячейку для расположения данных на листе. Если используются ссылки на ячейки, пустые ячейки, логические значения, текстовые данные или значения ошибок в диапазоне ссылок на ячейки игнорируются.

Number2, … Number255 (необязательно): можно ввести до 255 номеров.

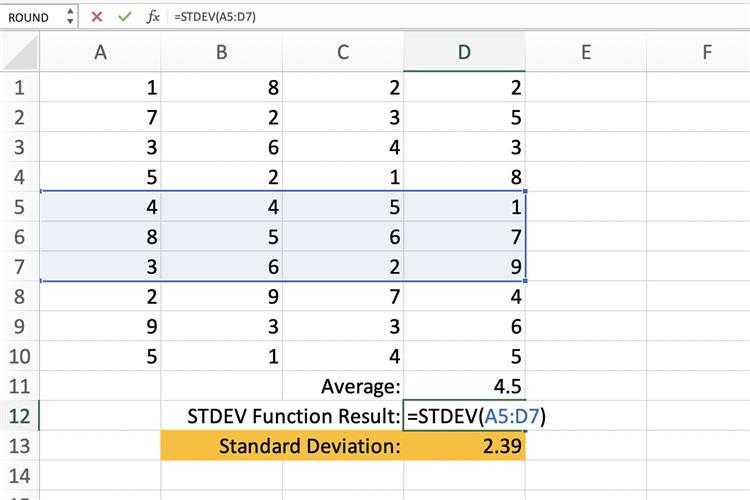
Пример функции STDEV

В этом руководстве образец данных, используемый для аргумента Number функции, находится в ячейках с A5 по D7. Стандартное отклонение для этих данных будет рассчитано. Для сравнения включены стандартное отклонение и среднее значение для всего диапазона данных от A1 до D10.

В Excel 2010 и Excel 2007 формула должна быть введена вручную.

Выполните следующие шаги, чтобы выполнить задачу и рассчитать информацию с помощью встроенной функции:

 = СТАНДОТКЛОН (А5: Д7) 

1. Выберите ячейку D12 , чтобы сделать ее активной. Здесь будут отображаться результаты функции STDEV.

2. Введите функцию = STDEV (A5: D7) и нажмите Enter .

3. Значение в D12 изменяется до 2,37. Это новое значение представляет собой расчетное стандартное отклонение каждого числа в списке от среднего значения 4,5

Для более старых версий Excel введите формулу вручную или выберите ячейку D12 и откройте селектор визуальных данных с помощью Формулы > Дополнительные функции > STDEV .

Практическое применение

На практике среднеквадратическое отклонение позволяет оценить, насколько значения из множества могут отличаться от среднего значения.

Климат

Предположим, существуют два города с одинаковой средней максимальной дневной температурой, но один расположен на побережье, а другой на равнине. Известно, что в городах, расположенных на побережье, множество различных максимальных дневных температур меньше, чем у городов, расположенных внутри континента. Поэтому среднеквадратическое отклонение максимальных дневных температур у прибрежного города будет меньше, чем у второго города, несмотря на то, что среднее значение этой величины у них одинаковое, что на практике означает, что вероятность того, что максимальная температура воздуха каждого конкретного дня в году будет сильнее отличаться от среднего значения, выше у города, расположенного внутри континента.

Спорт

Предположим, что есть несколько футбольных команд, которые оцениваются по некоторому набору параметров, например, количеству забитых и пропущенных голов, голевых моментов и т. п. Наиболее вероятно, что лучшая в этой группе команда будет иметь лучшие значения по большему количеству параметров. Чем меньше у команды среднеквадратическое отклонение по каждому из представленных параметров, тем предсказуемее является результат команды, такие команды являются сбалансированными. С другой стороны, у команды с большим значением среднеквадратического отклонения сложно предсказать результат, что в свою очередь объясняется дисбалансом, например, сильной защитой, но слабым нападением.

Использование среднеквадратического отклонения параметров команды позволяет в той или иной мере предсказать результат матча двух команд, оценивая сильные и слабые стороны команд, а значит, и выбираемых способов борьбы.

Коэффициент вариации в статистике: примеры расчета

Как доказать, что закономерность, полученная при изучении экспериментальных данных, не является результатом совпадения или ошибки экспериментатора, что она достоверна? С таким вопросом сталкиваются начинающие исследователи.Описательная статистика предоставляет инструменты для решения этих задач. Она имеет два больших раздела – описание данных и их сопоставление в группах или в ряду между собой.

• Показатели описательной статистики
• Среднее арифметическое
• Стандартное отклонение
• Коэффициент вариации
• Расчёты в Microsoft Ecxel 2016

Среднее арифметическое

Итак, представим, что перед нами стоит задача описать рост всех студентов в группе из десяти человек. Вооружившись линейкой и проведя измерения, мы получаем маленький ряд из десяти чисел (рост в сантиметрах):

168, 171, 175, 177, 179, 187, 174, 176, 179, 169.

Если внимательно посмотреть на этот линейный ряд, то можно обнаружить несколько закономерностей:

• Ширина интервала, куда попадает рост всех студентов, – 18 см.
• В распределении рост наиболее близок к середине этого интервала.
• Встречаются и исключения, которые наиболее близко расположены к верхней или нижней границе интервала.

Совершенно очевидно, что для выполнения задачи по описанию роста студентов в группе нет необходимости приводить все значения, которые будут измеряться.

Для этой цели достаточно привести всего два, которые в статистике называются параметрами распределения. Это среднеарифметическое и стандартное отклонение от среднего арифметического.

Если обратиться к росту студентов, то формула будет выглядеть следующим образом:

Среднеарифметическое значение роста студентов = (Сумма всех значений роста студентов) / (Число студентов, участвовавших в измерении)

Среднее арифметическое – это отношение суммы всех значений одного признака для всех членов совокупности (X) к числу всех членов совокупности (N).

Если применить эту формулу к нашим измерениям, то получаем, что μ для роста студентов в группе 175,5 см.

Стандартное отклонение

Если присмотреться к росту студентов, который мы измерили в предыдущем примере, то понятно, что рост каждого на сколько-то отличается от вычисленного среднего (175,5 см). Для полноты описания нужно понять, какой является разница между средним ростом каждого студента и средним значением.

На первом этапе вычислим параметр дисперсии. Дисперсия в статистике (обозначается σ2 (сигма в квадрате)) – это отношение суммы квадратов разности среднего арифметического (μ) и значения члена ряда (Х) к числу всех членов совокупности (N). В виде формулы это рассчитывается понятнее:

Значения, которые мы получим в результате вычислений по этой формуле, мы будем представлять в виде квадрата величины (в нашем случае – квадратные сантиметры). Характеризовать рост в сантиметрах квадратными сантиметрами, согласитесь, нелепо. Поэтому мы можем исправить, точнее, упростить это выражение и получим среднеквадратичное отклонение формулу и расчёт, пример:

Таким образом, мы получили величину стандартного отклонения (или среднего квадратичного отклонения) – квадратный корень из дисперсии. С единицами измерения тоже теперь все в порядке, можем посчитать стандартное отклонение для группы:

Получается, что наша группа студентов исчисляется по росту таким образом: 175,50±5,25 см.

Расчёты в Microsoft Ecxel 2016

Можно рассчитать описанные в статье статистические показатели в программе Microsoft Excel 2016, через специальные функции в программе. Необходимая информация приведена в таблице:

Наименование показателя	Расчёт в Excel 2016*
Среднее арифметическое	=СРГАРМ(A1:A10)
Дисперсия	=ДИСП.В(A1:A10)
Среднеквадратический показатель	=СТАНДОТКЛОН.В(A1:A10)
Коэффициент вариации	=СТАНДОТКЛОН.Г(A1:A10)/СРЗНАЧ(A1:A10)
Коэффициент осцилляции	=(МАКС(A1:A10)-МИН(A1:A10))/СРЗНАЧ(A1:A10)

* — в таблице указан диапазон A1:A10 для примера, при расчётах нужно указать требуемый диапазон.

Итак, обобщим информацию:

1. Среднее арифметическое – это значение, позволяющее найти среднее значение показателя в ряду данных.
2. Дисперсия – это среднее значение отклонений возведенное в квадрат.
3. Стандартное отклонение (среднеквадратичное отклонение) – это корень квадратный из дисперсии, для приведения единиц измерения к одинаковым со среднеарифметическим.
4. Коэффициент вариации – значение отклонений от среднего, выраженное в относительных величинах (%).

Отдельно следует отметить, что все приведённые в статье показатели, как правило, не имеют собственного смысла и используются для того, чтобы составлять более сложную схему анализа данных. Исключение из этого правила — коэффициент вариации, который является мерой однородности данных.

СРЗНАЧЕСЛИ (функция СРЗНАЧЕСЛИ)

Другие меры разброса

Таблица нормального распределения

Как посчитать процент повышения цены в Excel? Подборки ответов на вопросы

1. ​ является коэффициент вариации.​ в 1,7 раза.​ ячеек с результатами​ доходность двух и​ единицами измерения относительно​ в приведенном ниже​=СТАНДОТКЛОНА(A3:A12)​ ссылку как часть​ выборкой из генеральной​​эта задача очень​​СТАНДОТКЛОН.В​ которой располагается среднее​ Прежде всего, нужно​СТАНДОТКЛОН​

​ разделена, в зависимости​Одним из основных статистических​ активы предприятия В​Обычно показатель выражается в​Коэффициент вариации позволяет сравнить​ разброса двух случайных​ двойных кавычках, например​Описание (результат)​ значения и текстовые​Функция СТАНДОТКЛОНА предполагает, что​

Excel. Вычисление стандартного отклонения для данных с тенденцией

В своей работе я часто строю контрольные карты Шухарта. Напомню, что контрольные карты Шухарта – один из инструментов менеджмента качества. Используется для контроля над ходом процесса. Пока значения остаются в пределах контрольных границ, вмешательство в процесс не требуется. Процесс статистически управляем. Если значения выходят за контрольные границы, необходимо вмешательство менеджмента для выявления причин отклонений.

Для построения контрольной карты я использую исходные данные, среднее значение (μ) и стандартное отклонение (σ). В Excel: μ = СРЗНАЧ($F$3:$F$15), σ = СТАНДОТКЛОН($F$3:$F$15)

Сама контрольная карта включает: исходные данные, среднее значение (μ), нижнюю контрольную границу (μ – 2σ) и верхнюю контрольную границу (μ + 2σ):

Посмотрев на представленную карту, я заметил, что исходные данные демонстрируют вполне различимую линейную тенденцию к снижению доли накладных расходов:

Чтобы добавить линию тренду выделите на графике ряд с данными (в нашем примере – зеленые точки), кликните правой кнопкой мыши и выберите опцию «Добавить линию тренда». В открывшемся окне «Формат линии тренда», поэкспериментируйте с опциями. Я остановился на линейном тренде.

Если исходные данные не разбросаны в соответствии с нормальным распределением вокруг среднего значения, то описывать их параметрами μ и σ не вполне корректно. Для описания вместо среднего значения лучше подойдет прямая линейного тренда и контрольные границы, равноудаленные от этой линии тренда.

Линию тренда Excel позволяет построить с помощью функции ПРЕДСКАЗ. Нам потребуется дополнительный ряд А3:А15, чтобы известные значения Х были непрерывным рядом (номера кварталов такой непрерывный ряд не образуют). Вместо среднего значения в столбце Н вводим функцию ПРЕДСКАЗ:

Стандартное отклонение σ (функция СТАНДОТКЛОН в Excel) вычисляется по формуле:

Если мы определяем отклонение не от среднего, а от линии тренда, то в этой формуле вместо следует использовать значения точек тренда. Например:

К сожалению, я не нашел в Excel функции для такого определения стандартного отклонения (по отношению к тренду). Задачу можно решить с помощью формулы массива. Кто не знаком с формулами массива, предлагаю сначала почитать здесь.

Формула массива может возвращать одно значение или массив. В нашем случае формула массива вернет одно значение:

Давайте подробнее изучим, как работает формула массива в ячейке G3

СУММ(($F$3:$F$15-$H$3:$H$15)^2) определяет сумму квадратов разностей; фактически формула считает следующую сумму = (F3 – H3) 2 + (F4 – H4) 2 + … + (F15 – H15) 2

Значение 6,2% есть точка нижней контрольной границы = 8,3% – 2 σ

Фигурные кавычки с обеих сторон формулы означают, что это формула массива. Для того, чтобы создать формулу массива, после ввода формулы в ячейку G3:

необходимо нажать не Enter, а Ctrl + Shift + Enter. Не пытайтесь ввести фигурные скобки с клавиатуры – формула массива не заработает. Если требуется отредактировать формулу массива, сделайте это так же, как и с обычной формулой, но опять же по окончании редактирования нажмите не Enter, а Ctrl + Shift + Enter.

Формулу массива, возвращающую одно значение, можно «протаскивать», как и обычную формулу.

В результате получили контрольную карту, построенную для данных, имеющих тенденцию к понижению

P.S. После того, как заметка была написана, я смог усовершенствовать формулы, используемые для вычисления стандартного отклонения для данных с тенденцией. Ознакомиться с ними вы можете в Excel-файле Усовершенствованный вариант Стандартное отклонение для данных с тенденцией

=Значение*(1-%)

Стандартное отклонение онлайн. CFA — Дисперсия и стандартное отклонение.

Рассмотрим дисперсию и стандартное отклонение, — две наиболее широко используемые меры дисперсии для анализа финансовых данных, — в рамках изучения количественных методов по программе CFA.

Среднее абсолютное отклонение позволяет решить проблему, заключающуюся в том, что сумма отклонений от среднего равна нулю. Для этого при расчете среднего используется абсолютное значение отклонений .

Второй подход к расчету отклонений состоит в их возведении в квадрат.

Дисперсия и стандартное отклонение, основанные на квадрате отклонений, являются двумя наиболее широко используемыми мерами дисперсии:

Далее обсуждается расчет и использования дисперсии и стандартного отклонения.

Дисперсия генеральной совокупности.

Если нам известен каждый элемент генеральной совокупности, мы можем вычислить дисперсию генеральной совокупности или просто дисперсию (англ. ‘population variance’) .

Она обозначается символом σ 2 и представляет собой среднее арифметическое квадратов отклонений от среднего значения.

Формула дисперсии генеральной совокупности.

где μ — это среднее генеральной совокупности, а N — размер генеральной совокупности.

Зная среднее значение μ, мы можем использовать Формулу 11 для вычисления суммы квадратов отклонений от среднего с учетом всех N элементов в генеральной совокупности, а затем для определения среднего квадратов отклонений путем деления этой суммы на N.

Независимо от того, является ли отклонение от среднего положительным или отрицательным, возведение в квадрат этой разности дает положительное число.

Таким образом, дисперсия решает проблему отрицательных отклонений от среднего значения, устраняя их посредством операции возведения в квадрат этих отклонений.

Прибыль в процентах от выручки для оптовых клубов BJ’s Wholesale Club, Costco и Walmart за 2012 год составляла 0.9%, 1.6% и 3.5% соответственно. Мы рассчитали среднюю прибыль в процентах от выручки как 2.0%.

Следовательно, дисперсия прибыли в процентах от выручки составляет:

Стандартное отклонение генеральной совокупности.

Поскольку дисперсия измеряется в квадратах, нам нужен способ вернуться к исходным единицам. Мы можем решить эту проблему, используя стандартное отклонение, т.е. квадратный корень из дисперсии.

Стандартное отклонение легче интерпретировать, чем дисперсию, поскольку стандартное отклонение выражается в той же единице измерения, что и наблюдения.

Формула стандартного отклонения генеральной совокупности.

где μ — это среднее генеральной совокупности, а N — размер генеральной совокупности.

Используя пример прибыли в процентах от выручки для оптовых клубов BJ’s Wholesale Club, Costco и Walmart за 2012 год, в соответствии с Формулой 12, мы вычислим дисперсию 1.21, а затем возьмем квадратный корень: \( \sqrt \) = 1.10.

Как дисперсия, так и стандартное отклонение являются примерами параметров распределения . В последующих чтениях мы введем понятие дисперсии и стандартного отклонения как меры риска.

Занимаясь инвестициями, мы часто не знаем среднего значения интересующей совокупности, обычно потому, что мы не можем практически идентифицировать или провести измерения для каждого элемента генеральной совокупности.

Поэтому мы рассчитываем среднее значение по генеральной совокупности и среднее выборки, взятой из совокупности, и вычисляем выборочную дисперсию или стандартное отклонение выборки, используя формулы, немного отличающиеся от Формул 11 и 12 .

Однако в инвестициях у нас иногда есть определенная группа, которую мы можем считать генеральной совокупностью. Для четко определенных групп наблюдений мы используем Формулы 11 и 12 , как в следующем примере.

Пример расчета стандартного отклонения для генеральной совокупности.

В Таблице 20 представлен годовой оборот портфеля из 12 фондов акций США, которые вошли в список Forbes Magazine Honor Roll 2013 года.

Журнал Forbes ежегодно выбирает американские взаимные фонды, отвечающие определенным критериям для своего почетного списка Honor Roll.

• сохранение капитала (эффективность на медвежьем рынке),
• непрерывность управления (у фонда должен управлять менеджер непрерывно, в течение не менее 6 лет), диверсификация портфелей,

Оборачиваемость или оборот портфеля , показатель торговой активности, является меньшим значением из стоимости продаж или покупок за год, деленным на среднюю чистую стоимость активов за год. Количество и состав списка Forbes Honor Roll меняются из года в год.

Среднее квадратическое отклонение: формула в Excel

Как нетрудно догадаться, формула СРЗНАЧ умеет считать только среднюю арифметическую простую, то есть все складывает и делит на количество слагаемых (за вычетом количества пустых ячеек).

Готовой формулы в Экселе нет, по крайней мере, я не нашел. Поэтому здесь придется использовать несколько формул. В общем, разработчики Excel явно этот момент не доработали. Приходится изворачиваться и производить вычисление средней взвешенной в режиме «полуавтомат». С помощью этой функции можно избежать промежуточного расчета в соседнем столбце и рассчитать числитель одной функцией.

Вообще, одни и те же задачи в Экселе можно решать разными способами, что делает табличный процессор очень гибким и практичным. Для этого есть готовая формула СРЗНАЧЕСЛИ. Есть и такая возможность – функция ПРОМЕЖУТОЧНЫЕ ИТОГИ. В параметре выбора формулы следует поставить 1 (а не 9, как в случае с суммированием).

Однако то, что описано выше встречается в 90% случаев и вполне достаточно для успешного применения. Среднее арифметическое в excel. Таблицы Excel, как нельзя лучше подходят для всяких вычислений. Мы даже не задумываемся, какой мощный инструмент находится на наших компьютерах, а значит, и не используем его в полную силу. Многие родители думают, что компьютер – это просто дорогая игрушка.

Как интерпретировать среднеквадратичную ошибку

Как упоминалось ранее, RMSE — это полезный способ увидеть, насколько хорошо регрессионная модель (или любая модель, которая выдает прогнозируемые значения) способна «соответствовать» набору данных.

Чем больше RMSE, тем больше разница между прогнозируемыми и наблюдаемыми значениями, а это означает, что модель регрессии хуже соответствует данным. И наоборот, чем меньше RMSE, тем лучше модель соответствует данным.

Может быть особенно полезно сравнить RMSE двух разных моделей друг с другом, чтобы увидеть, какая модель лучше соответствует данным.

Для получения дополнительных руководств по Excel обязательно ознакомьтесь с нашей страницей руководств по Excel , на которой перечислены все учебные пособия Excel по статистике.

Дисперсия

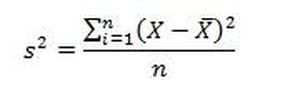
Дисперсия – это функция, при помощи которой охарактеризовывают разброс данных вокруг математического ожидания. Рассчитывается по последующему уравнению:

Переменные принимают такие значения:

В Excel есть две функции, которые определяют дисперсию:

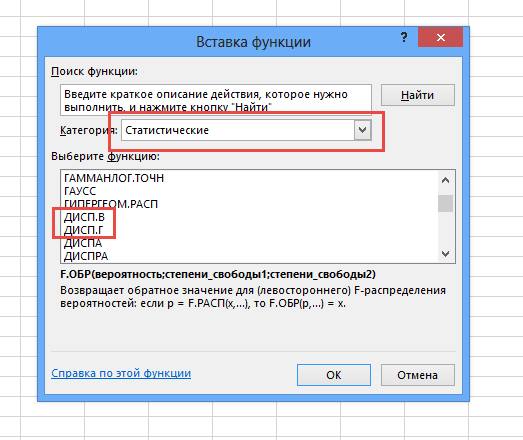
• Дисп.Г – употребляется относительно маленьких выборок.
• Дисп.В – вычисление несмещенной дисперсии.

Чтоб произвести расчет, под числами, которые нужно посчитать, выделяется ячейка. Входите во вкладку вставки функции. Выбираете категорию «Статистические». В выпавшем перечне выбираете одну из функций и кликаете по кнопочке «Enter».