Описательная статистика в excel. (лекция 4)

Основные показатели описательной статистики в Excel

Описательная статистика в Excel предоставляет ряд основных показателей, которые помогают описать и анализировать данные. Эти показатели включают среднее значение, медиану, моду, дисперсию, стандартное отклонение и квартили.

Среднее значение — это сумма всех значений в выборке, деленная на количество наблюдений. Он является одним из самых распространенных и простых показателей описательной статистики. Среднее значение может помочь понять средний уровень переменной и сравнить значения между различными группами или временными периодами.

Медиана — это значение, разделяющее выборку на две равные части. Если упорядочить значения по возрастанию (или убыванию) и выбрать средний элемент, то это и будет медиана. Медиану часто используют в случае, когда данные имеют выбросы или не подчиняются нормальному распределению.

Мода — это значение или значения, которые встречаются наиболее часто в выборке. Например, если среди наблюдений есть несколько значений, которые повторяются больше всего раз, то такие значения и являются модой. Мода особенно полезна при работе с категориальными переменными.

Дисперсия — это мера разброса данных относительно их среднего значения. Она показывает, насколько значения разбросаны вокруг среднего. Чем больше дисперсия, тем больший разброс данных. Если дисперсия равна нулю, то все значения одинаковы.

Стандартное отклонение — это квадратный корень из дисперсии. Оно показывает, насколько в среднем отдельные значения отклоняются от среднего значения. Стандартное отклонение может помочь определить стабильность данных и уровень риска.

Квартили — это значения, которые делят упорядоченную выборку на четыре равные части. Первый квартиль (25-й процентиль) указывает значение, ниже которого находится 25% наблюдений, а третий квартиль (75-й процентиль) указывает значение, ниже которого находится 75% наблюдений. Второй квартиль (50-й процентиль) соответствует медиане.

Используя данные показатели описательной статистики в Excel, можно получить полноценный анализ данных, легко определить основные характеристики и визуально представить результаты с помощью графиков и диаграмм.

3.2 Корреляционный анализ рядов динамики

Корреляционный анализ заключается в определении степени тесноты связи
между факторным и результативным признаком.

Различают следующие виды корреляционной зависимости:

парная корреляция, при которой изучается зависимость результативного
признака от одного факторного признака или двумя факторными признаками;

частная корреляция, при которой изучается зависимость результативного
признака от одного факторного признака при фиксированном значение других
факторных признаков;

множественная корреляция, при которой изучается зависимость
результативного признака от двух и более факторных признаков.

Связь между факторным и результативным признаком классифицируют по
аналитическому выражению, направлению и степени тесноты связи.

Корреляционный анализ дает возможность установить, ассоциированы ли
наборы данных по величине, то есть, большие значения из одного набора данных
связаны с большими значениями другого набора (положительная корреляция), или,
наоборот, малые значения одного набора связаны с большими значениями другого
(отрицательная корреляция), или данные двух диапазонов никак не связаны (корреляция
близка к нулю).

3.2.1 Расчет
коэффициента парной корреляции

Пример
№2. Имеются данные фондовых индексов Dowjons65 и Nasdaq100. Используя данные
представленные в таблице исходных данных (см. приложение) рассчитать
коэффициент парной корреляции между данными индексами.

Алгоритм решения следующий:

СервисАнализ данныхКорреляцияOK;

Выделяем
входной диапазон (Ссылка на диапазон, содержащий анализируемые данные. Ссылка
должна состоять не менее чем из двух смежных диапазонов данных, данные в
которых расположены по строкам или столбцам);

Устанавливаем
галочку напротив Метки в первой строке (Если первая строка исходного диапазона
содержит названия столбцов, установите переключатель в положение Метки в первой
строке. Если названия строк находятся в первом столбце входного диапазона,
установите переключатель в положение Метки в первом столбце. Если входной
диапазон не содержит меток, то необходимые заголовки в выходном диапазоне будут
созданы автоматически);

Устанавливаем
выходной диапазон (ссылка на левую верхнюю ячейку выходного диапазона.
Поскольку коэффициент корреляции двух наборов данных не зависит от
последовательности их обработки, то выходная область занимает только половину
предназначенного для нее места. Ячейки выходного диапазона, имеющие совпадающие
координаты строк и столбцов, содержат значение 1, так как каждая строка или
столбец во входном диапазоне полностью коррелирует с самим собой.) OK.

Если
каждый шаг был выполнен верно, то коэффициент корреляции должен быть равен
R2=0,954. Такое значение коэффициента парной корреляции свидетельствует о
сильной прямой зависимости между изучаемыми индексами.

статистический анализ динамика ряд

3.2.2 Расчет
коэффициента множественной корреляции

Пакет анализа данных позволяет решить более сложную задачу, связанную с
расчетом коэффициента множественной корреляции.

Пример №3. Допустим необходимо определить зависимость между USD и двумя
факторными признаками Forex и Euro.

Алгоритм действий следующий:

Выполняем те же шаги, что и в примере №3, только во входной диапазон
выделяем три столбца, со значениями признаков (USD, Euro, Forex).

Множественный коэффициент корреляции для двух факторных признаков
рассчитывается по формуле:

Рассчитав
парные коэффициенты между тремя признаками (см. таблицу ниже), подставляем
полученные коэффициенты в формулу множественного коэффициента корреляции.

Таблица
2

	FOREX(x1)	USD(y)	EURO(x2)
FOREX(x1)	1
USD(y)	-0,82027962	1
EURO(x2)	0,695326432	-0,791664	1

Описательная статистика в Excel: анализ данных

Описательная статистика в Excel – это мощный инструмент, который позволяет анализировать данные и получать полезную информацию о них. С помощью описательной статистики вы можете узнать основные характеристики данных, такие как среднее значение, медиана, минимальное и максимальное значения, дисперсия и стандартное отклонение.

Для использования описательной статистики в Excel вам понадобится набор данных, который вы хотите проанализировать. Этот набор данных может быть представлен в виде списка или таблицы.

Шаг 1: Открытие набора данных в Excel

Первым шагом является открытие набора данных в Excel. Для этого выберите пункт “Открыть” в меню “Файл” и выберите файл, содержащий ваш набор данных. Если у вас нет готового файла, вы можете ввести данные в таблицу Excel.

Шаг 2: Создание таблицы с данными

Для проведения анализа данных вам потребуется создать таблицу с данными. Вы можете использовать столбцы для представления различных переменных, а строки – для различных наблюдений. Присвойте заголовки столбцам для ясности.

Шаг 3: Выбор данных для анализа

Перед проведением анализа данных вам потребуется выбрать конкретные данные или переменные для анализа. На основе выбранных данных Excel будет строить описательную статистику.

Шаг 4: Использование функций Excel для получения описательной статистики

Excel предлагает несколько функций, которые могут быть использованы для получения описательной статистики ваших данных. Некоторые из этих функций включают AVERAGE (среднее значение), MEDIAN (медиана), MIN (минимальное значение), MAX (максимальное значение), VAR (дисперсия) и STDEV (стандартное отклонение).

Чтобы использовать эти функции, выберите ячейку, в которую вы хотите поместить результат, а затем введите функцию, указав диапазон ячеек, содержащих данные для анализа. Например, чтобы получить среднее значение числового столбца A1:A10, вы можете ввести формулу =AVERAGE(A1:A10).

Шаг 5: Визуализация данных

Помимо получения числовых значений описательной статистики, Excel также позволяет визуализировать данные с помощью графиков. Например, можно построить гистограмму, ящик с усами или график рассеивания данных. Графическое представление данных может помочь лучше понять их распределение и особенности.

Пример таблицы с данными:

№
Имя
Возраст
Зарплата

1
Иван
25
30000

2
Мария
30
35000

3
Алексей
28
32000

4
Елена
27
31000

В данном примере мы имеем таблицу с данными о людях, включающую их имена, возраст и зарплату. Мы можем использовать описательную статистику в Excel, чтобы получить средний возраст, максимальную зарплату и другие характеристики этого набора данных.

Таким образом, описательная статистика в Excel позволяет провести анализ данных и получить полезную информацию о них. Она может быть использована для выявления трендов, аномалий или закономерностей в данных, что поможет принимать обоснованные решения.

Функция СТЬЮДЕНТ.ТЕСТ()

Функция СТЬЮДЕНТ.ТЕСТ() используется для оценки различия двух выборочных средних . До MS EXCEL 2010 имелась аналогичная функция ТТЕСТ() .

Примечание : В английской версии функция носит название T.TEST(), старая версия — TTEST().

Функция СТЬЮДЕНТ.ТЕСТ() имеет 4 параметра. Первые два – это ссылки на диапазоны ячеек, содержащие выборки из 2-х сравниваемых распределений.

Третий параметр имеет название «хвосты». Этот параметр задает тип проверяемой гипотезы: односторонняя (=1) или двухсторонняя (=2). Если мы проверяем двухстороннюю гипотезу , то смотрим, не попало ли значение тестовой статистики в один из 2-х хвостов соответствующего t-распределения . Если мы проверяем одностороннюю гипотезу (имеется ввиду гипотеза μ ₁ файл примера ): =СТЬЮДЕНТ.ТЕСТ( выборка1 ; выборка2 ; 2; 3) или =2*(1-СТЬЮДЕНТ.РАСП(ABS(t *); v;ИСТИНА))

Для односторонней гипотезы μ ₁ =СТЬЮДЕНТ.ТЕСТ( выборка1 ; выборка2 ; 1; 3) или =СТЬЮДЕНТ.РАСП(t *; v;ИСТИНА)

Для односторонней гипотезы μ ₁ > μ ₂p -значение вычисляется по формуле: =1-СТЬЮДЕНТ.ТЕСТ( выборка1 ; выборка2 ; 1; 3) или =1-СТЬЮДЕНТ.РАСП(t *; v;ИСТИНА)

К сожалению, результаты, возвращаемые функцией СТЬЮДЕНТ.ТЕСТ() и формулой на основе функции СТЬЮДЕНТ.РАСП() незначительно отличаются (в 4-м знаке после запятой). Причем различие проявляется только для случая с неравными дисперсиями.

Какой результат правильный? В поддержку формулы на основе функции СТЬЮДЕНТ.РАСП() выступает надстройка Пакет анализа , которая возвращает аналогичный ей результат (см. ниже).

Здесь пригодится теория вероятности (probability theory).

Вероятность означает вероятность события, которое происходит, например, при наличии 3000 посетителей в день и выражается в процентах.

Самым распространенным примером вероятности, известным многим, является подбрасывание монеты. У монеты две стороны: орел и решка. Какова вероятность того, что монета ляжет той или другой стороной? Существует две возможности, таким образом 100%/2=50%

Достаточно теории, перейдет к практике.

Excel — прекрасный инструмент, который поможет нам в работе со статистикой. Отметим, что это не лучший инструмент, но зато все знают, как им пользоваться, поэтому рассмотрим именно Excel.

Во-первых, установите надсройку Analysis ToolPack.

Откройте Excel, перейдите в Опции -> Add-ins->внизу списка вы найдёте

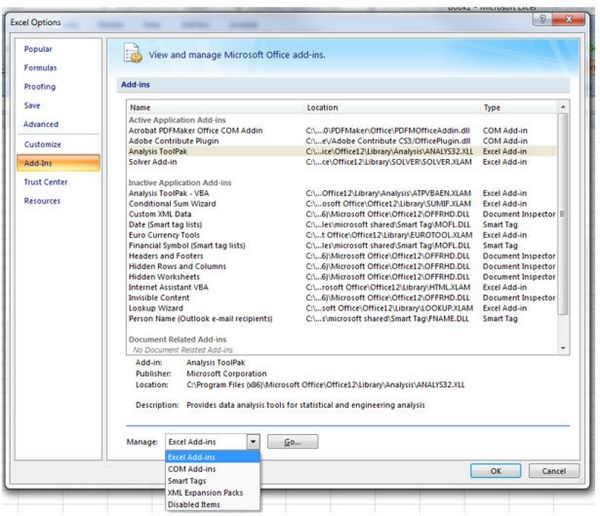
Нажимайте Go ->выберите Analysis ToolPack->и нажимайте OK.

Теперь в панеле выберите опцию Данные и найдите там Анализ данных.

Инструмент Анализ данных может предоставить вам невероятную статистическую информацию, но давайте начнем с чего-нибудь попроще.

Применение описательной статистики в Excel

Excel предоставляет мощные возможности для работы с описательной статистикой, позволяя быстро и эффективно проводить расчеты и визуализацию данных. С использованием различных функций и инструментов Excel можно легко определить среднее значение, медиану, дисперсию, стандартное отклонение и другие важные характеристики данных.

Одним из основных способов применения описательной статистики в Excel является проведение анализа данных в таблицах. С помощью фильтров, сортировки и группировки данных можно быстро и эффективно получить информацию о распределении данных по различным категориям и переменным.

Для визуализации данных и получения более наглядного представления о распределении можно использовать диаграммы и графики в Excel. Это позволяет легко отображать основные характеристики данных, такие как среднее значение, медиана и дисперсия, и сравнивать их между различными категориями и переменными.

Excel также предоставляет возможность проведения статистического анализа данных, включая расчеты вероятности, t-тесты, анализ дисперсии и многое другое. С использованием функций и инструментов Excel можно быстро и легко проводить сложные статистические вычисления и получать информацию о существенности и статистической значимости различных переменных и факторов.

В целом, применение описательной статистики в Excel является неотъемлемой частью работы с данными и анализа информации. С помощью различных функций и инструментов Excel можно легко проводить анализ данных, получать важные характеристики и визуализировать результаты, что позволяет принимать обоснованные и информированные решения на основе данных.

Пример таблицы со студенческими оценками
Имя студента	Оценка
Алексей	4
Елена	5
Иван	4
Мария	3

Приведенная выше таблица представляет собой пример данных, которые могут быть использованы для проведения анализа с помощью описательной статистики в Excel. С помощью различных функций и инструментов Excel можно рассчитать среднюю оценку, медиану, дисперсию и другие характеристики данных, а также визуализировать результаты для лучшего понимания и анализа.

Условия применения t-критерия Стьюдента

Несмотря на то, что открытие Стьюдента в свое время совершило переворот в статистике, t-критерий все же довольно сильно ограничен в возможностях применения, т.к. сам по себе происходит из предположения о нормальном распределении исходных данных. Если данные не являются нормальными (что обычно и бывает), то и t-критерий уже не будет иметь распределения Стьюдента. Однако в силу действия центральной предельной теоремы средняя даже у ненормальных данных быстро приобретает колоколообразную форму распределения.

Рассмотрим, для примера, данные, имеющие выраженный скос вправо, как у распределения хи-квадрат с 5-ю степенями свободы.

Теперь создадим 20 тысяч выборок и будет наблюдать, как меняется распределение средних в зависимости от их объема.

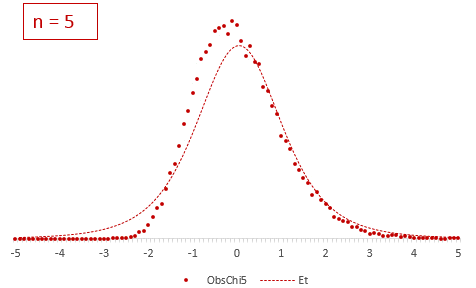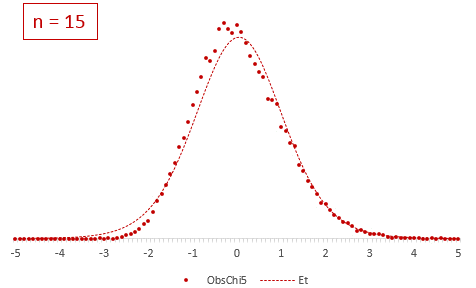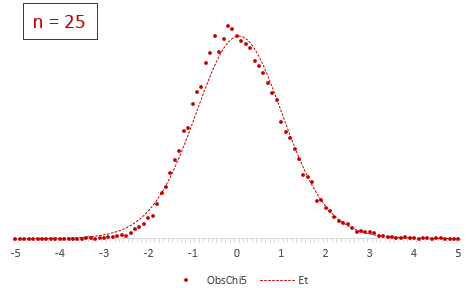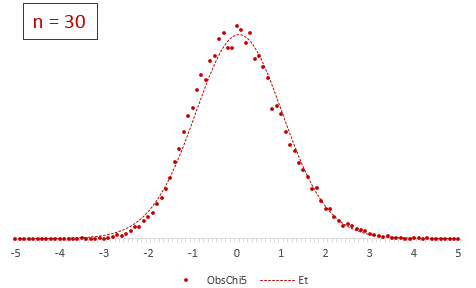
Отличие довольно заметно в малых выборках до 15-20-ти наблюдений. Но дальше оно стремительно исчезает. Таким образом, ненормальность распределения – это, конечно, нехорошо, но некритично.

Больше всего t-критерий «боится» выбросов, т.е. аномальных отклонений. Возьмем 20 тыс. нормальных выборок по 15 наблюдений и в часть из них добавим по одному случайном выбросу.

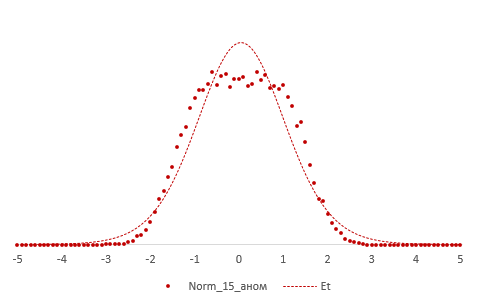
Картина получается нерадостная. Фактические частоты средних сильно отличаются от теоретических. Использование t-распределения в такой ситуации становится весьма рискованной затеей.

Итак, в не очень малых выборках (от 15-ти наблюдений) t-критерий относительно устойчив к ненормальному распределению исходных данных. А вот выбросы в данных сильно искажают распределение t-критерия, что, в свою очередь, может привести к ошибкам статистического вывода, поэтому от аномальных наблюдений следует избавиться. Часто из выборки удаляют все значения, выходящие за пределы ±2 стандартных отклонения от средней.

Статистика Excel: удивительно способна

Хотя Excel не известен своей статистической мощью, он на самом деле обладает некоторыми действительно полезными функциями. Особенно после того, как вы загрузите надстройку статистики Data Toolpak. Я надеюсь, что вы узнали, как использовать Toolpak, и теперь вы можете поиграть самостоятельно, чтобы выяснить, как использовать больше его функций.

Имея это в своем распоряжении, перенесите свои навыки работы с Excel на новый уровень с нашими статьями об использовании функции поиска целей в Excel для дополнительного анализа данных, освоения операторов IF в Excel и добавления раскрывающихся списков в виде ячеек в Excel.

Я также ссылался на другие сайты, на которых есть хорошие учебные пособия по статистике, где нам пришлось пропустить запутанные концепции. Обязательно ознакомьтесь с нашим руководством по бесплатным статистическим ресурсам

, тоже.

Корреляция в Excel

Чтобы вычислить корреляцию в Excel, можно использовать функцию CORREL. Эта функция принимает два аргумента: диапазон первой переменной и диапазон второй переменной. Например, чтобы вычислить корреляцию между стоимостью домов и их площадью, можно использовать следующую формулу:

Здесь A2:A10 — диапазон значений стоимости домов, а B2:B10 — диапазон значений площади домов.

Функция CORREL возвращает значение корреляции между двумя переменными в диапазоне от -1 до 1. Значение -1 означает полную отрицательную корреляцию, 1 — положительную корреляцию, а 0 — отсутствие корреляции.

Чтобы визуально представить корреляцию между двумя переменными, можно использовать диаграмму рассеяния. Диаграмма рассеяния — это график, на котором каждая точка представляет собой одну пару значений двух переменных. Зависимость между переменными можно оценить по общему тренду точек — если они расположены примерно на одной прямой линии, то переменные сильно коррелируют, если точки расположены случайно — корреляция слабая или отсутствует.

Для построения диаграммы рассеяния в Excel нужно выделить диапазон значений двух переменных и выбрать соответствующую опцию во вкладке «Вставка» на главной панели инструментов.

Корреляция	Интерпретация
-1	полная отрицательная корреляция
-0.7	высокая отрицательная корреляция
-0.3	умеренная отрицательная корреляция
отсутствие корреляции
0.3	умеренная положительная корреляция
0.7	высокая положительная корреляция
1	полная положительная корреляция

Функция CORREL также позволяет вычислять матрицу корреляции для нескольких переменных. В этом случае необходимо передать ей диапазон значений всех переменных. Функция вернет квадратную таблицу, в которой строки и столбцы соответствуют переменным, а каждая ячейка содержит коэффициент корреляции между соответствующими переменными.

МИН()/МАКС() и НАИБОЛЬШИЙ()/НАИМЕНЬШИЙ()

На первый взгляд, разница между этими функциями не особо прослеживается, хотя зачем их используют – очевидно – найти самое большое или маленькое число. Однако, в работе этих функций есть небольшая, но очень полезная разница. Разберем подробней.

Функция МИН() просто принимает массив аргументов и находит самое маленькое число. МАКС() – самое большое. Все просто.

Функция НАИМЕНЬШИЙ() же находит n-ое наименьшее число в массиве. НАИБОЛЬШИЙ(), наоборот, находит n-ое наибольшее число.

Например, нужно найти пятое по величине число. Вводим:

Фактически, получается, что результат работы НАИБОЛЬШИЙ(массив;1) и МАКС(массив) – одно и то же. Аналогичная ситуация с НАИМЕНЬШИЙ(массив;1) и МИН(массив).

Рекомендуем записаться на наш открытый онлайн-курс «Аналитика в Excel», если вы хотите научиться выполнять рутинную работу быстрее.

Как использовать описательную статистику

Описательная статистика – это метод анализа данных, который позволяет описать основные характеристики набора данных. В Excel есть несколько инструментов, которые позволяют использовать описательную статистику для анализа данных.

1. Среднее значение

Среднее значение – это сумма всех значений в наборе данных, разделенная на количество этих значений. В Excel можно найти среднее значение, используя функцию СРЗНАЧ.

Пример использования функции СРЗНАЧ:

Выберите ячейку, в которую хотите поместить результат.
Введите формулу вида “=СРЗНАЧ(диапазон_ячеек)”, где “диапазон_ячеек” – это диапазон данных, для которых нужно найти среднее значение.
Нажмите Enter, чтобы вычислить среднее значение.

2. Медиана

Медиана – это значение, которое разделяет набор данных на две равные части. В Excel можно найти медиану, используя функцию МЕДИАН.

Пример использования функции МЕДИАН:

Выберите ячейку, в которую хотите поместить результат.
Введите формулу вида “=МЕДИАН(диапазон_ячеек)”, где “диапазон_ячеек” – это диапазон данных, для которых нужно найти медиану.
Нажмите Enter, чтобы вычислить медиану.

3. Минимальное и максимальное значение

Минимальное и максимальное значение – это наименьшее и наибольшее значение в наборе данных соответственно. В Excel можно найти минимальное и максимальное значение, используя функции МИН и МАКС.

Пример использования функции МИН:

Выберите ячейку, в которую хотите поместить результат.
Введите формулу вида “=МИН(диапазон_ячеек)”, где “диапазон_ячеек” – это диапазон данных, для которых нужно найти минимальное значение.
Нажмите Enter, чтобы вычислить минимальное значение.

Пример использования функции МАКС:

Выберите ячейку, в которую хотите поместить результат.
Введите формулу вида “=МАКС(диапазон_ячеек)”, где “диапазон_ячеек” – это диапазон данных, для которых нужно найти максимальное значение.
Нажмите Enter, чтобы вычислить максимальное значение.

4. Стандартное отклонение и дисперсия

Стандартное отклонение и дисперсия – это меры разброса данных вокруг их среднего значения. В Excel можно найти стандартное отклонение и дисперсию, используя функции СТАНДОТКЛ и ДИСП.

Пример использования функции СТАНДОТКЛ:

Выберите ячейку, в которую хотите поместить результат.
Введите формулу вида “=СТАНДОТКЛ(диапазон_ячеек)”, где “диапазон_ячеек” – это диапазон данных, для которых нужно найти стандартное отклонение.
Нажмите Enter, чтобы вычислить стандартное отклонение.

Пример использования функции ДИСП:

Выберите ячейку, в которую хотите поместить результат.
Введите формулу вида “=ДИСП(диапазон_ячеек)”, где “диапазон_ячеек” – это диапазон данных, для которых нужно найти дисперсию.
Нажмите Enter, чтобы вычислить дисперсию.

5. Квартили

Квартили – это значения, которые разделяют набор данных на четыре равные части. В Excel можно найти квартили, используя функцию КВАРТИЛЬ.

Пример использования функции КВАРТИЛЬ:

Выберите ячейку, в которую хотите поместить результат.
Введите формулу вида “=КВАРТИЛЬ(диапазон_ячеек, номер_квартиля)”, где “диапазон_ячеек” – это диапазон данных, для которых нужно найти квартиль, и “номер_квартиля” – это число от 0 до 4, указывающее, какой квартиль нужно найти (0 – минимальный, 1 – первый квартиль, 2 – медиана, 3 – третий квартиль, 4 – максимальный).
Нажмите Enter, чтобы вычислить квартиль.

6. Размах

Размах – это разница между максимальным и минимальным значением в наборе данных. В Excel можно найти размах, вычитая минимальное значение из максимального.

Пример расчета размаха:

Выберите ячейку, в которую хотите поместить результат.
Вычитайте минимальное значение из максимального значения.

Описательная статистика помогает понять, как распределены данные и какие основные характеристики имеют. Используйте эти инструменты в Excel для анализа данных и принятия обоснованных решений на основе набора данных.

СРЗНАЧ() и СРЗНАЧА()

Редко кто задумывался, а ведь вычисление среднего значения – сугубо статистическая процедура: именно поэтому это операция и помещена в статистический пакет.

Наверно, особо не стоит останавливаться на правилах использования формулы: функция СРЗНАЧ() принимает на вход массив аргументов и дает на выходе среднее значение по всем ячейкам, содержащим числа(!). Это очень важный момент, который далеко не все знают. Поясним на примере.

Пусть дан диапазон А1:С2 и мы ищем среднее значение по всем 6 ячейкам диапазона:

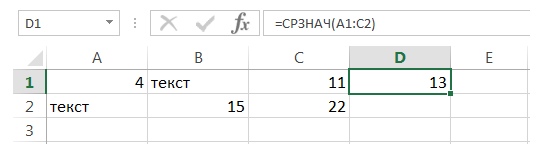Применение функции СРЗНАЧ()

Однако, результат функции СРЗНАЧ(А1:С2) будет не 8,7, а 13. Почему? (4+15+11+22)/6 = 8,7 ведь?

Да, это правильно, но функция СРЗНАЧ() берет в расчет только те ячейки, где «встречает» числа. Текстовая информация и пустые ячейки просто игнорируются. Поэтому в данном примере СРЗНАЧ() усредняет по 4 ячейкам и выдает правильный ответ – 13.

А вот если нужно произвести усреднение по всему диапазону, вне зависимости от типа данных, нужно использовать функцию СРЗНАЧА().

Принцип работы такой же, как и у СРЗНАЧ(), только на вход будут поступать абсолютно все ячейки. Результат в нашем примере будет уже ожидаемый – 8,7.

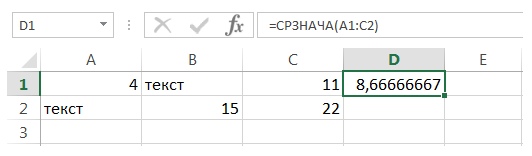Применение функции СРЗНАЧА()

Замечание

Выбор той или иной функции происходит в зависимости от задачи. В реальной жизни они могут понадобится в одинаковой мере.

Например, менеджеру нужно узнать среднедневную выручку за месяц на основании продаж за каждый день. Допустим, за несколько дней ячейки оставлены пустыми. Есть два варианта, почему так произошло:

1. В эти дни не было ни одной продажи. Тогда эти дни должны принимать участие в расчете среднего значения и менеджеру нужно использовать СРЗНАЧА() – так он исключит игнорирование пустых ячеек.

2. Эти дни были выходными. Тогда пропуски сами по себе никакой информации не несут и их надо игнорировать: фактически, эти дни не принимают участие в статистической выборке и функция СРЗНАЧ() поможет их пропустить.

КУРС

EXCEL ACADEMY

Научитесь использовать все прикладные инструменты из функционала MS Excel.