Расчет критерия стьюдента в excel

Как рассчитать «Доверительный интервал»?

Для того чтобы провести вычисления с использованием электронных таблиц, нужно вписать исследуемые значения в столбик. Далее выделяют отдельную ячейку, в которой расположится формула для вычислений и будет показан результат.

После того, как выбрана нужная клеточка, необходимо прибегнуть к помощи мастера. Его можно вызвать, нажав на кнопку, где есть обозначение «fx». После этого появится окно для выбора. Функции для вычисления доверительного интервала можно найти в категории статистических.

Её результат равен максимальной величине отклонения от среднего.

Таким образом, для получения левой границы доверительного интервала нужно из среднего значения вычесть полученное отклонение, а для правой — прибавить.

Функция ДОВЕРИТ.НОРМ

Эта функция присутствует в Excel, начиная с офиса 2010. До этого вместо неё использовалась ДОВЕРИТ(), которая от неё ничем не отличается.

При использовании мастера её нужно искать в разделе статистических.

Для того чтобы её использовать, надо ввести цифры в столбик и выбрать ячейку, в которой будут проводиться вычисления. Затем нажимают кнопку вызова мастера функций. Потребуется ввести три аргумента:

1. Первый называется «альфа». Здесь нужно указать вероятность, с какой случайная величина должна попадать внутрь искомого интервала. Обычно в условиях задачи её указывают в процентах. Пусть речь идёт о 95%. Нужный параметр получают по формуле (100 — Процент)/100, где Процент =95. В рассматриваемом случае альфа=0,05.
2. Здесь пишут стандартное отклонение. К моменту проведения вычислений оно должно быть известно. Это число является вторым параметром в формуле.
3. На третьем месте нужно указать количество полученных результатов. Эту цифру можно ввести руками, а можно для этого использовать СЧЁТ(), которая считает количество ячеек в выбранной области.

После того, как данные будут указаны, их надо подтвердить. После этого в выбранной клеточке будет получена половина длины полученного интервала (Дл).

Теперь надо вычислить среднюю величину (Ср). Это делают с помощью мастера функций, используя СРЕДН().

Теперь можно определить границы доверительного интервала. Для этого в одной из ячеек вычисляют Ср-Дл (левая граница), а в другой — Ср+Дл Правая граница.

При вычислении предполагается, что искомая случайная величина имеет нормальное распределение.

Функция ДОВЕРИТ.СТЮДЕНТ

Эта функция впервые появилась в Excel 2010. Раньше она не использовалась. Её применение во многом аналогично применению ДОВЕРИТ.НОРМ(), за исключением следующих особенностей:

1. Здесь используется не нормальное распределение, а распределение Стьюдента.
2. ДОВЕРИТ.СТЮДЕНТ() применяется в тех случаях, когда нет информации о том, чему равно стандартное отклонение. При этом оно вычисляется на основе предоставленных значений случайной величины.

Разница в использовании состоит в том, что при указании второго параметра пишут не число, а формулу для определения из имеющихся значений с использованием СТАНДОТКЛОН.В().

Остальные вычисления проводятся так же, как в предыдущем случае.

Алгоритм работы

_iСервис/Анализ данных/РегрессияxyМетки

1. Среднее значение: СРЗНАЧ(диапазон)
2. Квадратическое отклонение: КВАДРОТКЛ(диапазон)
3. Дисперсия: ДИСП(диапазон)
4. Дисперсия для генеральной совокупности: ДИСПР(диапазон)
5. Среднеквадратическое отклонение: СТАНДОТКЛОН(диапазон)
6. Уравнение регрессии y = b₁x₁+b₂x₂+. b_nx_n+b: ЛИНЕЙН(диапазон Y;диапазон X;1;1) .

Выделите блок ячеек размером (n+1) столбцов и 5 строк.

6. Коэффициенты множественной линейной регрессии вычисляются с помощью функции ЛИНЕЙН . Для того чтобы использовать эту функцию для вычисления параметров множественной регрессии необходимо 1) Сначала выделить на рабочем листе область размером 5x(k+1), где k — число объясняющих переменных. 2) Затем заполнить поля аргументов этой функции, которые имеют тот же смысл, что и в случае парной регрессии: Известные_значения_y — адреса ячеек, содержащих значения признака y; Известные_значения_x — адреса ячеек, содержащих значения всех объясняющих переменных

Обратите внимание: выборочные значения факторов должны располагаться рядом друг с другом (в смежной области), причем предполагается, что в первом столбце (строке) содержатся значения первой объясняющей переменной, во втором столбце — второй и т.д. Константа — значение (логическое), указывающее на наличие свободного члена в уравнении регрессии: укажите в поле Константа значение 1, тогда свободный член рассчитывается обычным образом (если значение поля Константа равно 0, то свободный член полагается равным 0); Статистика — значение (логическое), которое указывает на то, следует ли выводить дополнительную информацию по регрессионному анализу или нет: укажите в поле Статистика значение равное 1, тогда будет выводиться дополнительная регрессионная информация (если Статистика=0, то выводятся только оценки коэффициентов уравнения регрессии);. Критерий Фишера предназначен для сопоставления двух выборок по частоте встречаемости интересующего исследователя эффекта

Критерий Фишера предназначен для сопоставления двух выборок по частоте встречаемости интересующего исследователя эффекта.

При увеличении расхождения между углами φ1 и φ2 и увеличения численности выборок значение критерия возрастает. Чем больше величина φ*, тем более вероятно, что различия достоверны.

Гипотезы критерия Фишера

H: Доля лиц, у которых проявляется исследуемый эффект, в выборке 1 не больше, чем в выборке 2.

H₁: Доля лиц, у которых проявляется исследуемый эффект, в выборке 1 больше, чем в выборке 2.

Процедура вычисления

Этот метод используется при интервальной оценке различных статистических величин. Главная задача данного расчета – избавится от неопределенностей точечной оценки.

Способ 1: функция ДОВЕРИТ.НОРМ

Оператор ДОВЕРИТ.НОРМ, относящийся к статистической группе функций, впервые появился в Excel 2010. В более ранних версиях этой программы используется его аналог ДОВЕРИТ. Задачей этого оператора является расчет доверительного интервала с нормальным распределением для средней генеральной совокупности.

Его синтаксис выглядит следующим образом:

Все аргументы данного оператора являются обязательными.

Функция ДОВЕРИТ имеет точно такие же аргументы и возможности, что и предыдущая. Её синтаксис таков:

Как видим, различия только в наименовании оператора. Указанная функция в целях совместимости оставлена в Excel 2010 и в более новых версиях в специальной категории «Совместимость». В версиях же Excel 2007 и ранее она присутствует в основной группе статистических операторов.

Граница доверительного интервала определяется при помощи формулы следующего вида:

Где X – это среднее выборочное значение, которое расположено посередине выбранного диапазона.

Теперь давайте рассмотрим, как рассчитать доверительный интервал на конкретном примере. Было проведено 12 испытаний, вследствие которых были получены различные результаты, занесенные в таблицу. Это и есть наша совокупность. Стандартное отклонение равно 8. Нам нужно рассчитать доверительный интервал при уровне доверия 97%.

1. Выделяем ячейку, куда будет выводиться результат обработки данных. Щелкаем по кнопке «Вставить функцию».

Значит, чтобы посчитать уровень значимости, то есть, определить значение «Альфа» следует применить формулу такого вида:

То есть, подставив значение, получаем:

Путем нехитрых расчетов узнаем, что аргумент «Альфа» равен 0,03. Вводим данное значение в поле.

Как известно, по условию стандартное отклонение равно 8. Поэтому в поле «Стандартное отклонение» просто записываем это число.

В поле «Размер» нужно ввести количество элементов проведенных испытаний. Как мы помним, их 12. Но чтобы автоматизировать формулу и не редактировать её каждый раз при проведении нового испытания, давайте зададим данное значение не обычным числом, а при помощи оператора СЧЁТ. Итак, устанавливаем курсор в поле «Размер», а затем кликаем по треугольнику, который размещен слева от строки формул.

Группа аргументов «Значения» представляет собой ссылку на диапазон, в котором нужно рассчитать количество заполненных числовыми данными ячеек. Всего может насчитываться до 255 подобных аргументов, но в нашем случае понадобится лишь один.

Данный оператор предназначен для расчета среднего арифметического значения выбранного диапазона чисел. Он имеет следующий довольно простой синтаксис:

Аргумент «Число» может быть как отдельным числовым значением, так и ссылкой на ячейки или даже целые диапазоны, которые их содержат.

Способ 2: функция ДОВЕРИТ.СТЮДЕНТ

Кроме того, в Экселе есть ещё одна функция, которая связана с вычислением доверительного интервала – ДОВЕРИТ.СТЮДЕНТ. Она появилась, только начиная с Excel 2010. Данный оператор выполняет вычисление доверительного интервала генеральной совокупности с использованием распределения Стьюдента. Его очень удобно использовать в том случае, когда дисперсия и, соответственно, стандартное отклонение неизвестны. Синтаксис оператора такой:

Как видим, наименования операторов и в этом случае остались неизменными.

Посмотрим, как рассчитать границы доверительного интервала с неизвестным стандартным отклонением на примере всё той же совокупности, что мы рассматривали в предыдущем способе. Уровень доверия, как и в прошлый раз, возьмем 97%.

1. Выделяем ячейку, в которую будет производиться расчет. Клацаем по кнопке «Вставить функцию».

В поле «Альфа», учитывая, что уровень доверия составляет 97%, записываем число 0,03. Второй раз на принципах расчета данного параметра останавливаться не будем.

Как видим, инструменты программы Excel позволяют существенно облегчить вычисление доверительного интервала и его границ. Для этих целей используются отдельные операторы для выборок, у которых дисперсия известна и неизвестна.

Проверка статистической гипотезы позволяет сделать строгий вывод о характеристиках генеральной совокупности на основе выборочных данных. Гипотезы бывают разные. Одна из них – это гипотеза о средней (математическом ожидании). Суть ее в том, чтобы на основе только имеющейся выборки сделать корректное заключение о том, где может или не может находится генеральная средняя (точную правду мы никогда не узнаем, но можем сузить круг поиска).

Определение термина

Но для начала давайте все-таки выясним, что такое критерий Стьюдента вообще. Этот индикатор используется для проверки сходства между средними значениями двух выборок. То есть он определяет достоверность различий между двумя группами данных. При этом для определения этого критерия используется целый комплекс методов. Индикатор может рассчитываться с одно- или двусторонним распределением.

Что такое статистическая значимость?

Представьте, что вы хотите узнать, какая из двух ног дает наилучший результат. Вы бросаете первый кубик и получаете 2; вы бросаете второй кубик и получаете 6. Означает ли это, что второй кубик обычно дает больше очков? Если вы ответили «Конечно, нет», у вас уже есть некоторое представление о статистической значимости. Вы понимаете, что разница возникла из-за случайного изменения счета при каждом броске кости. Поскольку выборка была очень маленькой (всего один бросок), ничего существенного она не показала.

Теперь представьте, что вы бросаете каждый кубик 6 раз:

• Первые кости бросают 3, 6, 6, 4, 3, 3; Среднее = 4,17
• Второй бросает кубик 5, 6, 2, 5, 2, 4; Среднее = 4,00

Означает ли это, что первая кость дает больше очков, чем вторая? Возможно нет. Небольшая выборка с относительно небольшой разницей между средними делает вероятным, что разница все же обусловлена ​​случайной вариацией. По мере того, как мы увеличиваем количество бросков костей, становится трудно дать разумный ответ на вопрос — является ли разница между оценками результатом случайной вариации или на самом деле более вероятно, что один из них дает более высокий балл, чем другой?

Значимость — это вероятность того, что наблюдаемая разница между выборками обусловлена ​​случайными колебаниями. Это значение часто называют альфа-уровнем или просто «α». Уровень достоверности, или просто «s», — это вероятность того, что разница между выборками не связана со случайной вариацией; иными словами, существует разница между большими группами населения. Следовательно: c = 1 — α

Мы можем установить «α» на любой уровень, если хотим быть уверенными в том, что доказали свою ценность. Очень часто используется α = 5 % (достоверность 95 %), но если мы хотим быть абсолютно уверены, что любые различия не вызваны случайными колебаниями, мы можем использовать более высокий уровень достоверности, используя α = 1 % или даже α = 0,1 %.

Различные статистические тесты используются для расчета значимости в различных ситуациях. T-тесты используются, чтобы определить, различаются ли средние значения двух популяций, а F-тесты используются, чтобы определить, различаются ли средние значения .

Зачем проверять статистическую значимость?

Когда мы сравниваем разные вещи, мы должны использовать проверку значимости, чтобы выяснить, лучше ли одна вещь, чем другая. Это относится ко многим полям, например:

• В бизнесе людям приходится сравнивать различные продукты и методы маркетинга.
• В спорте людям приходится сравнивать различное оборудование, технику и соперников.
• В процессе разработки людям приходится сравнивать различные конструкции и настройки параметров.

Если вы хотите проверить, работает ли что-то лучше, чем что-то другое, в какой-либо области, вам необходимо проверить статистическую значимость.

Что такое T-распределение студента?

Распределение Стьюдента равно нормальному (или гауссовскому) распределению. Оба распределения имеют форму колокола, большинство из которых близки к среднему, но некоторые редкие события довольно далеки от среднего в любом направлении, которые называются хвостами распределения.

Точная форма распределения Стьюдента зависит от размера выборки. Для выборок более 30 это очень похоже на нормальное распределение. По мере уменьшения размера выборки хвосты становятся больше, отражая возросшую неопределенность, связанную с выводами из небольшой выборки.

How to Do a T-Test in Excel

Before you can apply a T-Test to determine whether there’s a statistically significant difference between the means of two samples, you must first perform an F-Test. This is because different calculations are performed for the T-Test depending on whether there’s a significant difference between the variances.

You will need the Analysis Toolpak add-in enabled to perform this analysis.

Checking and Loading the Analysis Toolpak Add-In

To check and activate the Analysis Toolpak follow these steps:

1. Select the FILE tab >select Options.

2. In the Options dialogue box, select Add-Ins from the tabs on the left-hand side.

3. At the bottom of the window, select the Manage drop-down menu, then select Excel Add-ins. Select Go.

4. Ensure the check-box next to Analysis Toolpak is checked, then select OK.

5. The Analysis Toolpak is now active and you are ready to apply F-Tests and T-Tests.

Статистический анализ роста доли дохода в Excel за период

Пример 2. В таблице приведены данные о доходах предпринимателя за год. Доказать, что примерно 75% значений меньше, чем третий квартиль доходов.

Вид исходной таблицы:

Определим 3-й по формуле:

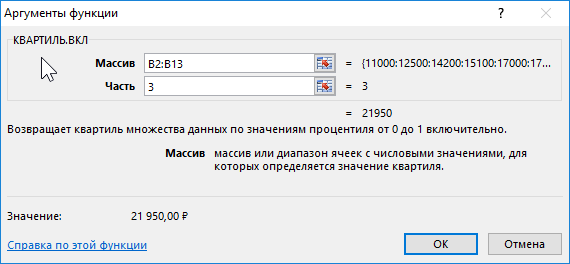
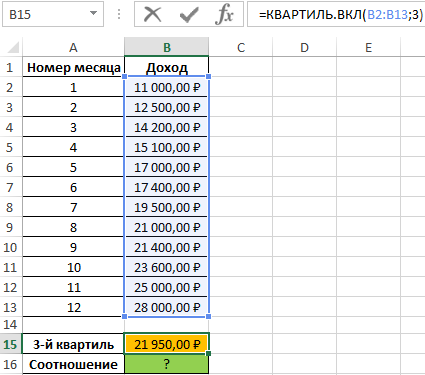
Определим соотношение чисел, меньше полученного числа, к общему количеству значений по формуле:

=СЧЁТЕСЛИ(B2:B13;” Пример 3. Имеется диапазон случайных чисел, отсортированный в порядке возрастания. Определить соотношение суммы чисел, которые меньше 1-го квартиля, к сумме чисел, которые превышают значение 1-го квартиля.

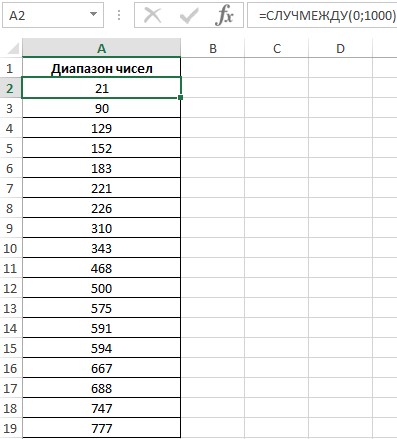
Чтобы сгенерировать случайное число в Excel воспользуемся функцией:

После генерации отсортируем случайно сгенерированные числа по возрастанию. Вид исходной таблицы данных со случайными числами:

Формула для расчета имеет следующий вид (формула массива CTRL+SHIFT+ENTER):

Функции СУММ с вложенными функциями ЕСЛИ выполняют расчет суммы только тех чисел, которые меньше и больше соответственно значения, возвращаемого функцией для исследуемого диапазона. Из полученных значений вычисляется частное. Результат расчетов:

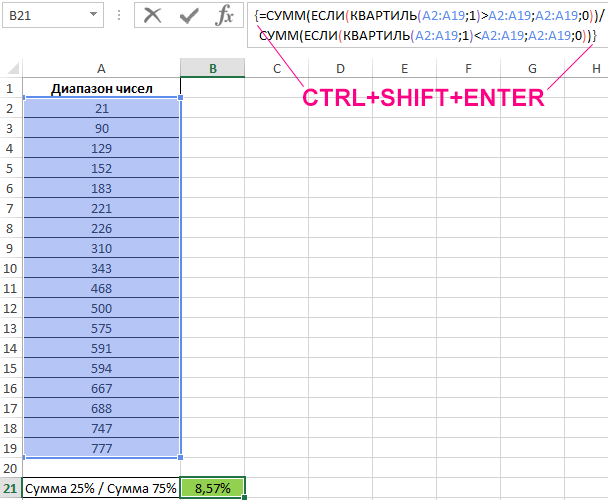
Общая сумма чисел исследуемого диапазона, которые меньше 1-го квартиля, составляет всего 8,57% от общей суммы чисел, которые больше 1-го квартиля.

Расчет квартилей в R и SAS

Функция quantile в R использует все девять алгоритмов расчета квантилей, в соответствии с нумерацией, предложенной Hyndman and Fan в работе 1996 г. (рис. 15; если вы не знакомы с R, рекомендую начать с Алексей Шипунов. Наглядная статистика. Используем R! ). Квантиль при i-м методе расчета:

Регрессионный анализ в excel

Формула для вычислений

Функция EXCEL или инструмент Анализа данных

Оценка параметров модели парной регрессии

Смысл аргументов функции

изв_знач_у – диапазон значений у;

изв_знач_х – диапазон значений х;

константа – устанавливается на 0, если заранее известно, что свободный член равен 0 и на 1 в противном случае;

стат – устанавливается на 0, если не нужен вывод дополнительных сведений регрессионного анализа и на 1 в противном случае.

Возвращает следующую информацию

Значение коэффициента b₁

Значение коэффициента b

Среднеквадратическое отклонение b₁

Среднеквадратическое отклонение b

Коэффициент детерминации R 2

Среднеквадратическое отклонение у

Число степеней свободы

Регрессионная сумма квадратов

Остаточная сумма квадратов

Оценка параметров модели парной и множественной линейной регрессии.

Для вычисления параметров уравнения регрессии следует воспользоваться инструментом Регрессия

Возвращает подробную информацию о параметрах модели, качестве модели, расчетных значениях и остатках в виде четырех таблиц: Регрессионная статистика, Дисперсионный анализ, Коэффициенты, ВЫВОД ОСТАТКА.

Так же может быть получен график подбора.

Оценка значимости параметров модели линейной регрессии с использованием t — критерия Стьюдента.

,

Вычисленное по этой формуле значение сравнивается с критическим значением t-критерия, которое берется из таблицы значений t Стьюдента с учетом заданного уровня значимости и числа степеней свободы (n-k-1), где k количество факторов в модели.

Вероятность — вероятность, соответствующая двустороннему распределению Стьюдента.

Степени_свободы — число степеней свободы, характеризующее распределение.

Возвращает t-значение распределения Стьюдента как функцию вероятности и числа степеней свободы.

Проверка значимости модели регрессии с использованием

Вероятность — это вероятность, связанная с F-распределением.

Степени_свободы 1 — это числитель степеней свободы-₁—k.

Степени_свободы 2 — это знаменатель степеней свободы-.₂ — (n — k — 1),

где k – количество факторов, включенных в модель,

Возвращает обратное значение для F-распределения вероятностей.

FРАСПОБР можно использовать, чтобы определить критические значения F-распределения.

Чтобы определить критическое значение F, нужно использовать уровень значимости как аргумент вероятность для FРАСПОБР.

Значения F-критерия Фишера при уровне значимости =0,05

Для того, чтобы рассчитать t-критерий Стьюдента (для зависимых и для независимых выборок) в Excell необходимо сделать следующие шаги:

1.Вносим значения для двух переменных в таблицу (Например Переменная 1 и Переменная 2)

2. Ставим курсор в пустую ячейку

3. На панеле инструментов нажимаем кнопку fx (вставить формулу)

4. В открывшемся окне «Мастер функций» в поле «Категории» выбираем Полный алфавитный перечень

5. Затем в поле «Выберите функцию» находим функцию TTECT, которая возвращает вероятность, соответствующую критерию Стьюдента.

5.1. Нажимаем Ок

6. В открывшемся окне «Аргументы функции» в поле Массив1 вносим номера ячеек, содержащие значения Переменной 1, в поле Массив2 вносим номера ячеек, содержащие значения Переменной2.

7. В поле «Хвосты» пишем 2 (критерий будет рассчитываться используя двустороннее распределение, как и в SPSS); либо 1 (критерий будет рассчитываться используя одностороннее распределение).

Важно! 8. В поле «Тип» пишем 1 (рассчитывается, если выборки зависимые); либо 2 или 3 (если выборки независимые)

Функция СТЮДРАСПОБР предназначена для расчета значения квантиля уровня, соответствующего известной вероятности (указывается в качестве первого аргумента), распределения Стьюдента для известных степеней свободы и возвращает обратное t-распределение.

Регрессионный анализ в Excel

Показывает влияние одних значений (самостоятельных, независимых) на зависимую переменную. К примеру, как зависит количество экономически активного населения от числа предприятий, величины заработной платы и др. параметров. Или: как влияют иностранные инвестиции, цены на энергоресурсы и др. на уровень ВВП.

Результат анализа позволяет выделять приоритеты. И основываясь на главных факторах, прогнозировать, планировать развитие приоритетных направлений, принимать управленческие решения.

• линейной (у = а + bx);
• параболической (y = a + bx + cx 2 );
• экспоненциальной (y = a * exp(bx));
• степенной (y = a*x^b);
• гиперболической (y = b/x + a);
• логарифмической (y = b * 1n(x) + a);
• показательной (y = a * b^x).

Рассмотрим на примере построение регрессионной модели в Excel и интерпретацию результатов. Возьмем линейный тип регрессии.

Задача. На 6 предприятиях была проанализирована среднемесячная заработная плата и количество уволившихся сотрудников. Необходимо определить зависимость числа уволившихся сотрудников от средней зарплаты.

Модель линейной регрессии имеет следующий вид:

Где а – коэффициенты регрессии, х – влияющие переменные, к – число факторов.

В нашем примере в качестве У выступает показатель уволившихся работников. Влияющий фактор – заработная плата (х).

В Excel существуют встроенные функции, с помощью которых можно рассчитать параметры модели линейной регрессии. Но быстрее это сделает надстройка «Пакет анализа».

Активируем мощный аналитический инструмент:

1. Нажимаем кнопку «Офис» и переходим на вкладку «Параметры Excel». «Надстройки».
2. Внизу, под выпадающим списком, в поле «Управление» будет надпись «Надстройки Excel» (если ее нет, нажмите на флажок справа и выберите). И кнопка «Перейти». Жмем.
3. Открывается список доступных надстроек. Выбираем «Пакет анализа» и нажимаем ОК.

После активации надстройка будет доступна на вкладке «Данные».

Теперь займемся непосредственно регрессионным анализом.

1. Открываем меню инструмента «Анализ данных». Выбираем «Регрессия».
2. Откроется меню для выбора входных значений и параметров вывода (где отобразить результат). В полях для исходных данных указываем диапазон описываемого параметра (У) и влияющего на него фактора (Х). Остальное можно и не заполнять.
3. После нажатия ОК, программа отобразит расчеты на новом листе (можно выбрать интервал для отображения на текущем листе или назначить вывод в новую книгу).

В первую очередь обращаем внимание на R-квадрат и коэффициенты. R-квадрат – коэффициент детерминации. В нашем примере – 0,755, или 75,5%

Это означает, что расчетные параметры модели на 75,5% объясняют зависимость между изучаемыми параметрами. Чем выше коэффициент детерминации, тем качественнее модель. Хорошо – выше 0,8. Плохо – меньше 0,5 (такой анализ вряд ли можно считать резонным). В нашем примере – «неплохо»

В нашем примере – 0,755, или 75,5%. Это означает, что расчетные параметры модели на 75,5% объясняют зависимость между изучаемыми параметрами. Чем выше коэффициент детерминации, тем качественнее модель. Хорошо – выше 0,8. Плохо – меньше 0,5 (такой анализ вряд ли можно считать резонным). В нашем примере – «неплохо»

R-квадрат – коэффициент детерминации. В нашем примере – 0,755, или 75,5%. Это означает, что расчетные параметры модели на 75,5% объясняют зависимость между изучаемыми параметрами. Чем выше коэффициент детерминации, тем качественнее модель. Хорошо – выше 0,8. Плохо – меньше 0,5 (такой анализ вряд ли можно считать резонным). В нашем примере – «неплохо».

Коэффициент 64,1428 показывает, каким будет Y, если все переменные в рассматриваемой модели будут равны 0. То есть на значение анализируемого параметра влияют и другие факторы, не описанные в модели.

Коэффициент -0,16285 показывает весомость переменной Х на Y. То есть среднемесячная заработная плата в пределах данной модели влияет на количество уволившихся с весом -0,16285 (это небольшая степень влияния). Знак «-» указывает на отрицательное влияние: чем больше зарплата, тем меньше уволившихся. Что справедливо.

Этапы статистического вывода (statistic inference)

1. Первый из них – это вопрос, который мы хотим изучить с помощью статистических методов. То есть первый этап: что изучаем? И какие у нас есть предположения относительно результата? Этот этап называется этап статистических гипотез.
2. Второй этап – нужно определиться с тем, какие у нас есть в реальности данные для того, чтобы ответить на первый вопрос. Этот этап – тип данных.
3. Третий этап состоит в том, чтобы выбрать корректный для применения в данной ситуации статистический критерий.
4. Четвертый этап это логичный этап применения интерпретации любой формулы, какие результаты мы получили.
5. Пятый этап это создание, синтез выводов относительно первого, второго, третьего, четвертого, пятого этапа, то есть что же получили и что же это в реальности значит.