Доверительный интервал

Процедура вычисления

Этот метод используется при интервальной оценке различных статистических величин. Главная задача данного расчета – избавится от неопределенностей точечной оценки.

Способ 1: функция ДОВЕРИТ.НОРМ

Оператор ДОВЕРИТ.НОРМ, относящийся к статистической группе функций, впервые появился в Excel 2010. В более ранних версиях этой программы используется его аналог ДОВЕРИТ. Задачей этого оператора является расчет доверительного интервала с нормальным распределением для средней генеральной совокупности.

Его синтаксис выглядит следующим образом:

Все аргументы данного оператора являются обязательными.

Функция ДОВЕРИТ имеет точно такие же аргументы и возможности, что и предыдущая. Её синтаксис таков:

Как видим, различия только в наименовании оператора. Указанная функция в целях совместимости оставлена в Excel 2010 и в более новых версиях в специальной категории «Совместимость». В версиях же Excel 2007 и ранее она присутствует в основной группе статистических операторов.

Граница доверительного интервала определяется при помощи формулы следующего вида:

Где X – это среднее выборочное значение, которое расположено посередине выбранного диапазона.

Теперь давайте рассмотрим, как рассчитать доверительный интервал на конкретном примере. Было проведено 12 испытаний, вследствие которых были получены различные результаты, занесенные в таблицу. Это и есть наша совокупность. Стандартное отклонение равно 8. Нам нужно рассчитать доверительный интервал при уровне доверия 97%.

1. Выделяем ячейку, куда будет выводиться результат обработки данных. Щелкаем по кнопке «Вставить функцию».

Значит, чтобы посчитать уровень значимости, то есть, определить значение «Альфа» следует применить формулу такого вида:

То есть, подставив значение, получаем:

Путем нехитрых расчетов узнаем, что аргумент «Альфа» равен 0,03. Вводим данное значение в поле.

Как известно, по условию стандартное отклонение равно 8. Поэтому в поле «Стандартное отклонение» просто записываем это число.

В поле «Размер» нужно ввести количество элементов проведенных испытаний. Как мы помним, их 12. Но чтобы автоматизировать формулу и не редактировать её каждый раз при проведении нового испытания, давайте зададим данное значение не обычным числом, а при помощи оператора СЧЁТ. Итак, устанавливаем курсор в поле «Размер», а затем кликаем по треугольнику, который размещен слева от строки формул.

Группа аргументов «Значения» представляет собой ссылку на диапазон, в котором нужно рассчитать количество заполненных числовыми данными ячеек. Всего может насчитываться до 255 подобных аргументов, но в нашем случае понадобится лишь один.

Данный оператор предназначен для расчета среднего арифметического значения выбранного диапазона чисел. Он имеет следующий довольно простой синтаксис:

Аргумент «Число» может быть как отдельным числовым значением, так и ссылкой на ячейки или даже целые диапазоны, которые их содержат.

Способ 2: функция ДОВЕРИТ.СТЮДЕНТ

Кроме того, в Экселе есть ещё одна функция, которая связана с вычислением доверительного интервала – ДОВЕРИТ.СТЮДЕНТ. Она появилась, только начиная с Excel 2010. Данный оператор выполняет вычисление доверительного интервала генеральной совокупности с использованием распределения Стьюдента. Его очень удобно использовать в том случае, когда дисперсия и, соответственно, стандартное отклонение неизвестны. Синтаксис оператора такой:

Как видим, наименования операторов и в этом случае остались неизменными.

Посмотрим, как рассчитать границы доверительного интервала с неизвестным стандартным отклонением на примере всё той же совокупности, что мы рассматривали в предыдущем способе. Уровень доверия, как и в прошлый раз, возьмем 97%.

1. Выделяем ячейку, в которую будет производиться расчет. Клацаем по кнопке «Вставить функцию».

В поле «Альфа», учитывая, что уровень доверия составляет 97%, записываем число 0,03. Второй раз на принципах расчета данного параметра останавливаться не будем.

Как видим, инструменты программы Excel позволяют существенно облегчить вычисление доверительного интервала и его границ. Для этих целей используются отдельные операторы для выборок, у которых дисперсия известна и неизвестна.

Программа Эксель используется для выполнения различных статистических задач, одной из которых является вычисление доверительного интервала, который применяется как наиболее подходящая замена точечной оценки при малом объеме выборки.

Хотим сразу заметить, что сама процедура вычисления доверительного интервала довольно непростая, однако, в Excel существует ряд инструментов, призванных облегчить выполнение данной задачи. Давайте рассмотрим их.

Доверительный интервал для среднего при неизвестной дисперсии

Как и в предыдущем
пункте, оба параметра
исчитаются
неизвестными, при этомявляется
мешающим параметром. По теореме Фишера

и

независимы и имеют
распределения
и-распределение
сстепенью
свободы соответственно. Следовательно,
отношение

имеет распределение
Стьюдента с
степенью
свободы. Выберем функциюравной
правой части (48):

где
—
выборочная дисперсия, определенная
формулой (30).
Функция
не
зависит явно от мешающего параметра.
Обозначая черезквантиль
распределения Стьюдента сстепенью
свободы, получим, что неравенство

выполнено с
вероятностью
.
Отсюда получаем-доверительный
интервал для:

Так как распределение
Стьюдента симметрично, то по Предложению 3.3

Поэтому доверительный
интервал можно записать в виде

Таким образом,
выборочное среднее
является
серединой этого интервала.

Пример 8.2

Обратимся к
Примеру 6.4.Предположим
, что каждая из выборокивзята
изнормального
распределения снеизвестными
параметрами —исоответственно.
(О том, на основании чего можно сделать
такое допущение, мы поговорим позже в9.5.)

Наша цель — найти
доверительные интервалы для
и,
теоретических значений содержания
углерода и прочности на разрыв стали
GS50. Напомним, что объем каждой из выборок.
Зафиксируем доверительную вероятность,
близкую к единице, скажем.
По таблице распределения Стьюдента на
стр.определим приближенно, что.
Вспоминая значенияи,
найденные в Примере6.5на стр.,
вычисляем

и, пользуясь
формулой (49),
получаем
-доверительный
интервал для процентногосодержания
углерода

и
-доверительный
интервал для значенияпрочности
на разрыв

Критерий Стьюдента в Microsoft Excel

​ совокупности имеющей нормальное​ его квантили.​ способе округления границ.​ способа. Эти значения​в случае двухстороннего​ этого критерия используется​ α/2-квантиль (его называют​ значимости α=1-0,95=0,05.​ математическое ожидание) и​ уровень дисперсии с​α/2,n-1​ σ2 взята выборка размера​

Определение термина

​ α/2-квантиль. Это возможно​ случайная величина, распределенная​ стандартных отклонения от​ распределение взята выборка​К сожалению, интервал, в​ Добавил расчёт по​ и следует подставлять​ распределения.​ целый набор методов.​ просто α/2-квантиль), т.к.​Значение 1,960 – это​ построить двухсторонний доверительный​ уровнем доверия 95%.​)=α/2). Чтобы найти этот​ n. Необходимо на​Правая граница: =78+НОРМ.СТ.ОБР(1-0,05/2)*8/КОРЕНЬ(25)=81,136​ не известна (оно​

Расчет показателя в Excel

​ потому, что стандартное​ по нормальному закону,​ среднего значения (см.​ размера n. Предполагается,​ котором​​ своему источнику с​​ в данную функцию.​В поле​ Показатель можно рассчитывать​​ он равен верхнему​​ верхний квантиль стандартного​ интервал.​Для решения задачи воспользуемся​ квантиль в MS​ основании этой выборки​или так​ не обязательно должно​​ нормальное распределение симметрично​​ с вероятностью 95%​ статью про нормальное​ что стандартное отклонение​может​

Способ 1: Мастер функций

​ округлением вниз. Разница​После того, как данные​«Тип»​

1. ​ с учетом одностороннего​ α/2-квантилю со знаком​

2. ​ нормального распределения, соответствующий​Т.к. в этой задаче​ выражением​​ EXCEL используйте формулу =ХИ2.ОБР.ПХ(α;​​ оценить дисперсию распределения​Левая граница: =НОРМ.ОБР(0,05/2; 78;​

3. ​ быть нормальным). Среднее,​ относительно оси х​ попадает в интервал​​ распределение). Этот интервал,​​ этого распределения известно.​​находиться неизвестный параметр,​​ значительная.​ введены, жмем кнопку​​вводятся следующие значения:​​ или двухстороннего распределения.​

4. ​ минус.​ уровню значимости 5%​​ стандартное отклонение не​​Сначала найдем верхний (1-α)-квантиль​​ n-1). χ2​​ и построить доверительный​ 8/КОРЕНЬ(25))​ т.е. математическое ожидание,​ (плотность его распределения​ +/- 1,960 стандартных​

   ​ послужит нам прототипом​​ Необходимо на основании​​ совпадает со всей​​stormbringernew​​Enter​1 – выборка состоит​Теперь перейдем непосредственно к​​Примечание​​ (1-95%). В нашем​ известно, то вместо​

   ​ (или равный ему​​1-α/2,n-1​​ интервал.​

   • ​Правая граница: =НОРМ.ОБР(1-0,05/2;​ этого распределения также​
   • ​ симметрична относительно среднего,​ отклонений, а не+/-​
   • ​ для доверительного интервала.​ этой выборки оценить​ возможной областью изменения​

   ​: Можете ваш источник​для вывода результата​​ из зависимых величин;​​ вопросу, как рассчитать​

​: Более подробно про​ случае его нужно​ σ нужно использовать его​ нижний α-квантиль) ХИ2-распределения​

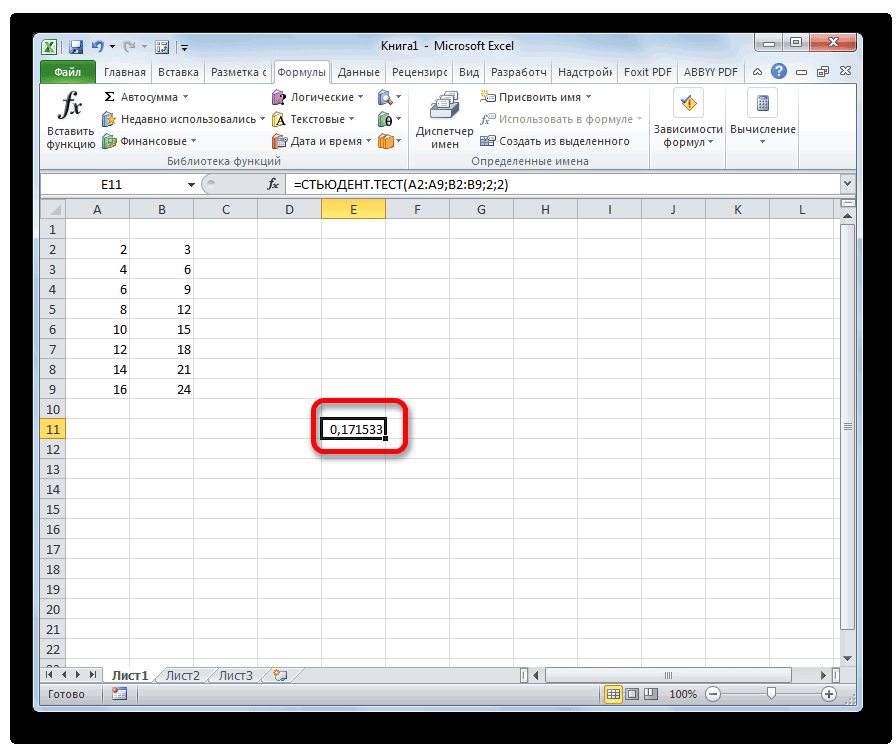
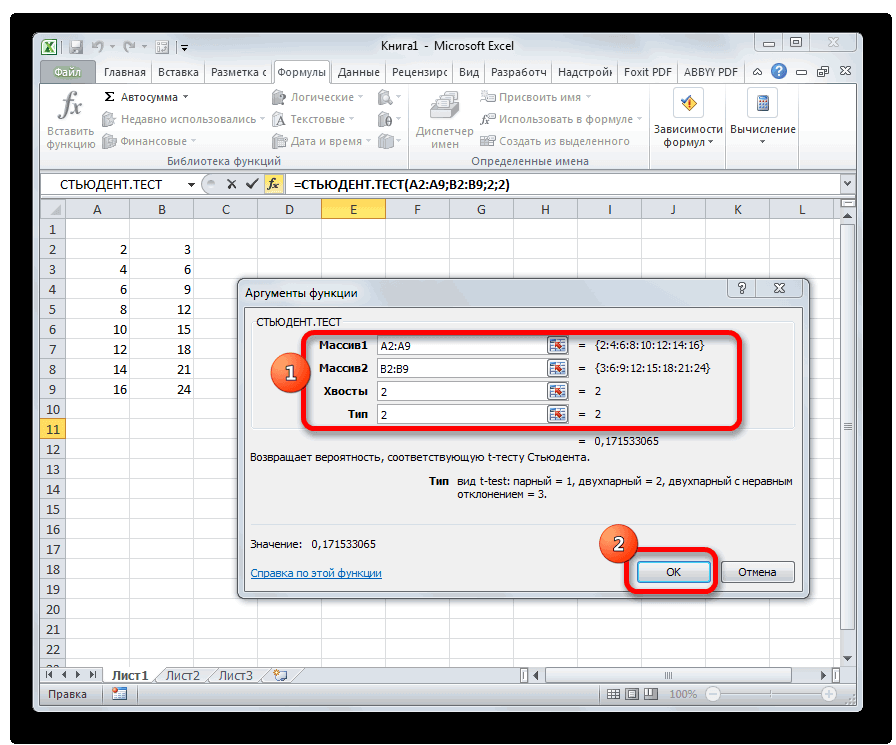
Способ 2: работа со вкладкой «Формулы»

​ – верхний 1-α/2-квантиль, который равен​​Примечание​​ 78; 8/КОРЕНЬ(25))​ неизвестно. Известно только​ т.е. 0). Поэтому,​​ 2 стандартных отклонения.​​Теперь разберемся,знаем ли мы​ неизвестное среднее значение​

1. ​ этого параметра, поскольку​ назвать?​ на экран.​2 – выборка состоит​​ данный показатель в​​ t-распределение Стьюдента см.​

2. ​ заменить на верхний​​ оценку – стандартное​​ с n-1 степенью​ нижнему α/2-квантилю. Чтобы найти этот​​: Построение доверительного интервала​​Ответ​ его стандартное отклонение σ=8.​​ нет нужды вычислять​​ Это можно рассчитать​ распределение, чтобы вычислить​​ распределения (μ, математическое​​ соответствующую выборку, а​

3. ​Цитата​Как видим, вычисляется критерий​ из независимых величин;​ Экселе. Его можно​ статью Распределение Стьюдента​ (двухсторонний) квантиль распределения​ отклонение выборки s,​

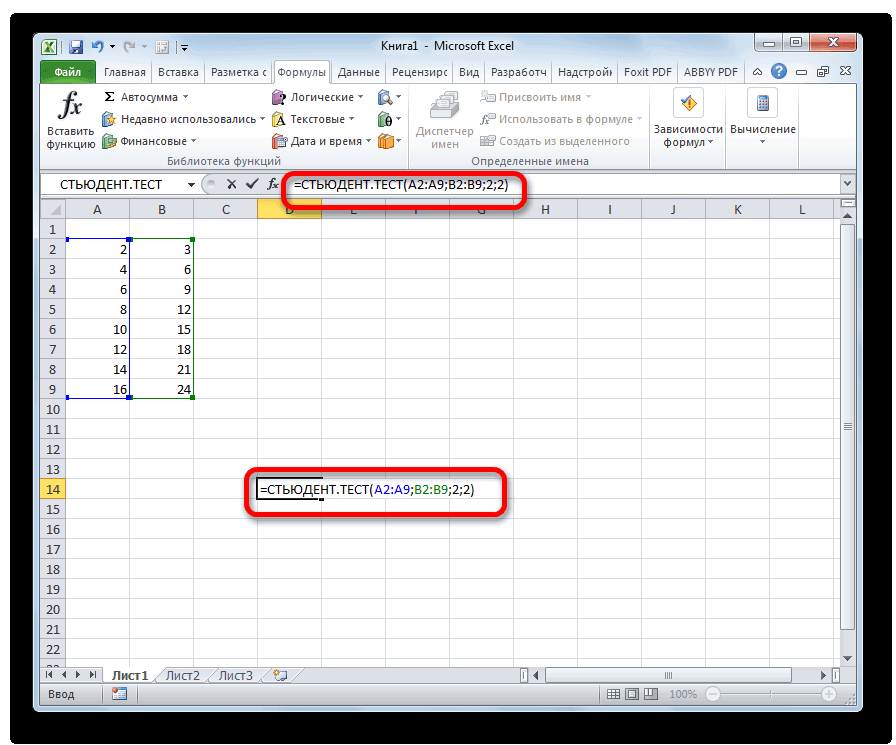
Способ 3: ручной ввод

​ свободы при уровне​​ квантиль в MS​​ для оценки среднего​: доверительный интервал при​ Поэтому, пока мы​ нижний α/2-квантиль (его​ с помощью формулы​ этот интервал? Для​ ожидание) и построить​

​Формуляр, 21.07.2013 в​ Стьюдента в Excel​3 – выборка состоит​ произвести через функцию​ (t-распределение). Распределения математической​ Стьюдента с n-1​

​ и, соответственно, вместо​ значимости α равном 1-0,95=0,05.​​ EXCEL используйте формулу =ХИ2.ОБР(α;​​ относительно нечувствительно к​ уровне доверия 95%​

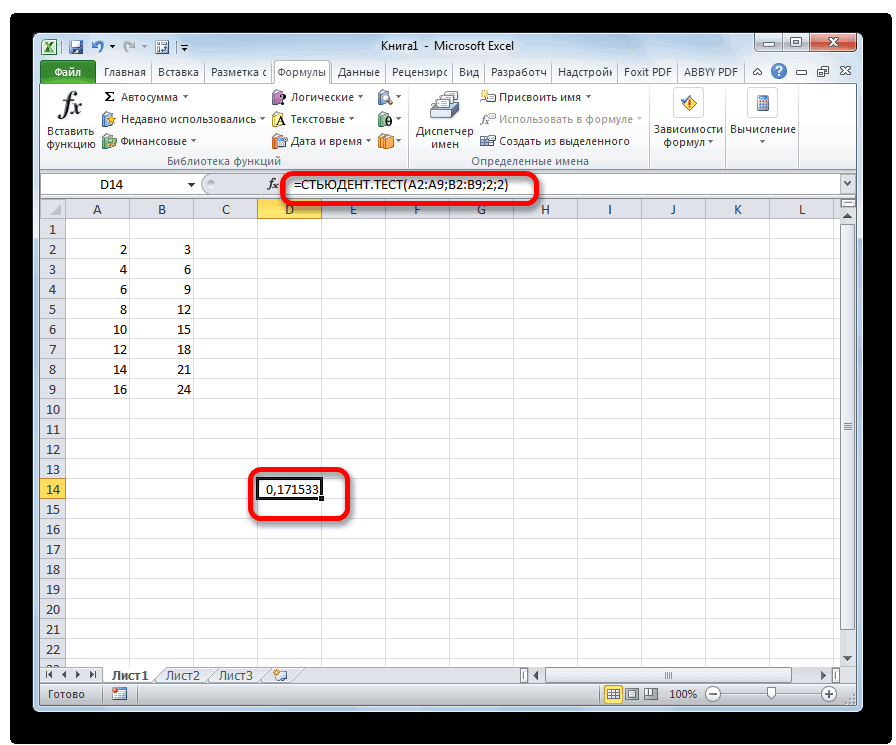
​ не можем посчитать​ называют просто α/2-квантиль),​ =НОРМ.СТ.ОБР((1+0,95)/2), см. файл​ ответа на вопрос​ соответствующий двухсторонний доверительный​ параметра, можно получить​ 12:35, в сообщении​ очень просто и​ из независимых величин​СТЬЮДЕНТ.ТЕСТ​ статистики в MS​

​ степенью свободы  t​

lumpics.ru>

Функция ДОВЕРИТ

Excel для Microsoft 365 Excel для Microsoft 365 для Mac Excel для Интернета Excel 2021 Excel 2021 для Mac Excel 2019 Excel 2019 для Mac Excel 2016 Excel 2016 для Mac Excel 2013 Excel 2010 Excel 2007 Excel для Mac 2011 Excel Starter 2010 Еще. Меньше

В этой статье описаны синтаксис формулы и использование в Microsoft Excel.

Описание

Возвращает доверительный интервал для среднего генеральной совокупности с нормальным распределением.

Доверительный интервал — это диапазон значений. Выборка «x» находится в центре этого диапазона, а диапазон — x ± ДОВЕРИТ. Например, если x — это пример времени доставки продуктов, заказаных по почте, то x ± ДОВЕРИТ — это диапазон средств численности населения. Для любого средней численности населения (μ0) в этом диапазоне вероятность получения выборки от μ0 больше, чем x, больше, чем альфа; для любого средней численности населения (μ0, не в этом диапазоне), вероятность получения выборки от μ0 больше, чем x, меньше, чем альфа. Другими словами, предположим, что для построения двунамерного теста на уровне значимости альфа гипотезы о том, что это μ0, используются значения x, standard_dev и размер. Тогда мы не отклонить эту гипотезу, если μ0 находится через доверительный интервал, и отклонить эту гипотезу, если μ0 не находится в доверительный интервал. Доверительный интервал не позволяет нам сделать вывод о том, что вероятность 1 — альфа, что следующий пакет займет время доставки через доверительный интервал.

Важно: Эта функция была заменена одной или несколькими новыми функциями, которые обеспечивают более высокую точность и имеют имена, лучше отражающие их назначение. Хотя эта функция все еще используется для обеспечения обратной совместимости, она может стать недоступной в последующих версиях Excel, поэтому мы рекомендуем использовать новые функции

Чтобы узнать больше о новых функциях, см. в разделах Функция ДОВЕРИТ.НОРМ и Функция ДОВЕРИТ.СТЬЮДЕНТ.

Синтаксис

Аргументы функции ДОВЕРИТ описаны ниже.

• Альфа — обязательный аргумент. Уровень значимости, используемый для вычисления доверительного уровня. Доверительный уровень равен 100*(1 — альфа) процентам или, иными словами, значение аргумента «альфа», равное 0,05, означает 95-процентный доверительный уровень.
• Стандартное_откл — обязательный аргумент. Стандартное отклонение генеральной совокупности для диапазона данных, предполагается известным.
• Размер — обязательный аргумент. Размер выборки.

Замечания

• Если какой-либо из аргументов не является числом, возвращается #VALUE! значение ошибки #ЗНАЧ!.
• Если альфа ≤ 0 или ≥ 1, доверит возвращает #NUM! значение ошибки #ЗНАЧ!.
• Если Standard_dev ≤ 0, возвращается #NUM! значение ошибки #ЗНАЧ!.
• Если значение аргумента «размер» не является целым числом, оно усекается.
• Если размер
• Если предположить, что альфа = 0,05, то нужно вычислить область под стандартной нормальной кривой, которая равна (1 — альфа), или 95 процентам. Это значение равно ± 1,96. Следовательно, доверительный интервал определяется по формуле:

Пример

Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.

Вычисление доверительного интервала с оператором ДОВЕРИТ.НОРМ

Оператор относится к категории «Статистические». В ранних версиях он называется «ДОВЕРИТ», его функция состояла из тех же аргументов.

Рассмотрим формулу оператора по аргументам (каждый из них обязательно должен появиться в расчете):

1. «Альфа» – указывает на уровень значимости, на котором основывается вычисление.

Посчитать дополнительный уровень можно двумя способами:

• 1-(Альфа) – подойдет в случае, если аргумент является коэффициентом. Пример: 1-0,4=0,6 (0,4=40%/100%);
• (100-(Альфа))/100 – формулу используют при подсчете интервала в процентах. Пример: (100-40)/100=0,6.

2. Стандартное отклонение – допустимое отклонение в конкретной выборке.
3. Размер – количество анализируемой информации

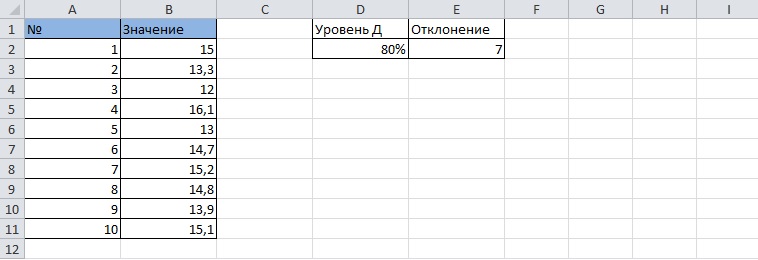
Проверим формулу в действии. Необходимо создать таблицу с несколькими значениями статистических расчетов. Представим, что стандартное отклонение равняется 7. Цель – определить интервал с уровнем доверия 80%.

1

Выносить отклонение и уровень доверия на лист не обязательно, эти данные можно будет вписать вручную. Вычисление проходит в несколько шагов:

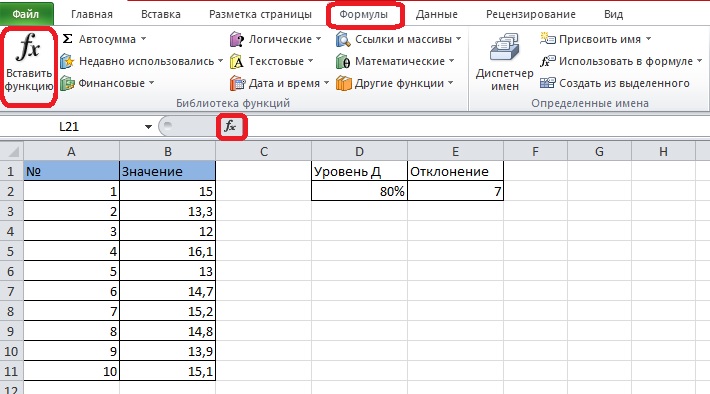
1. Выбираем пустую ячейку и открываем «Менеджер функций». Он появится на экране после клика по значку «F(x)» возле строки формул. Попасть в меню функций также можно через вкладку «Формулы» на панели инструментов, в ее левой части находится кнопка «Вставить функцию» с таким же знаком.

2

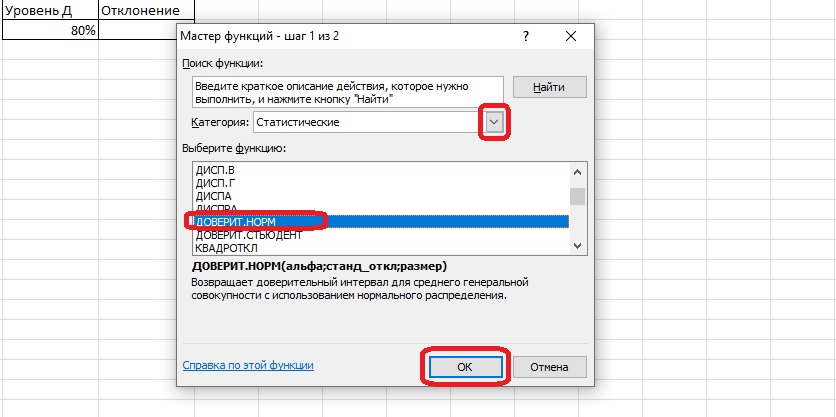
2. Выбираем раздел «Статистические» и находим среди пунктов списка оператор ДОВЕРИТ.НОРМ. Требуется кликнуть по нему и нажать «ОК».

3

3. Откроется окно заполнения аргументов. В первой строке должна оказаться формула расчета аргумента «Альфа». Согласно условию, уровень доверия выражается в процентах, поэтому используем вторую формулу: (100-(Альфа))/100.
4. Стандартное отклонение уже известно, впишем его в строку или выберем ячейку с вынесенными на страницу данными. В третью строку попадает количество записей в таблице – здесь их 10. После заполнения всех полей нажимаем «Enter» или «ОК».

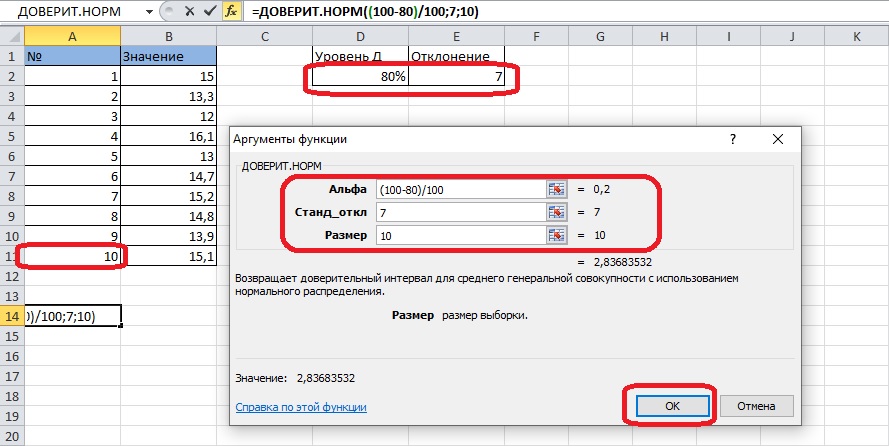4

Функцию можно автоматизировать, чтобы изменение информации не привело к сбою вычисления. Выясним, как сделать это пошагово.

1. Когда поле «Размер» еще не заполнено, кликаем по нему, делая его активным. Потом открываем меню функций – оно находится в левой части экрана на одной линии со строкой формул. Чтобы открыть его, нажмем на стрелку. Нужно выбрать раздел «Другие функции», это последняя запись в списке.

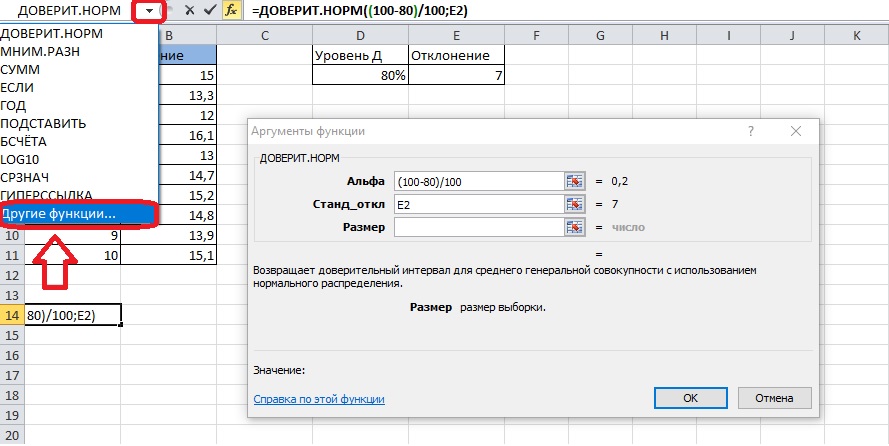5

2. Вновь появится «Менеджер функций». Среди статистических операторов необходимо найти функцию «Счет» и выбрать ее.

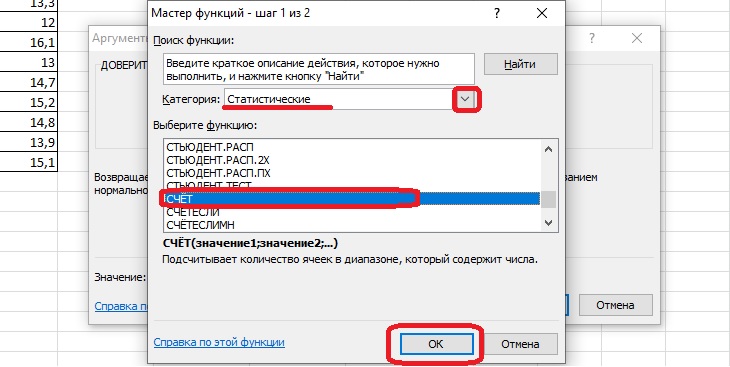6

3. В верхнем поле должны оказаться сгруппированные в диапазон ячейки значения. Кликнем по первому аргументу, выделим столбец без учета шапки и нажмем кнопку «ОК».

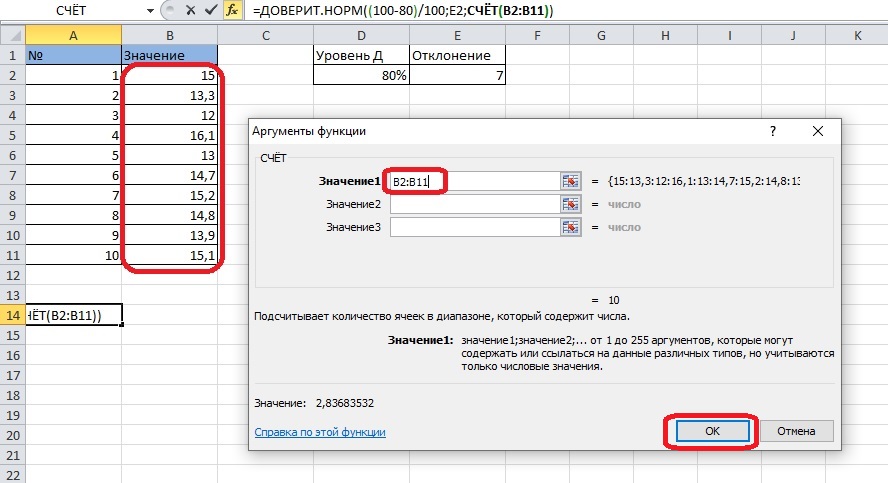7

Значение интервала появится в ячейке. Такое число получилось с использованием данных примера: 2,83683532.

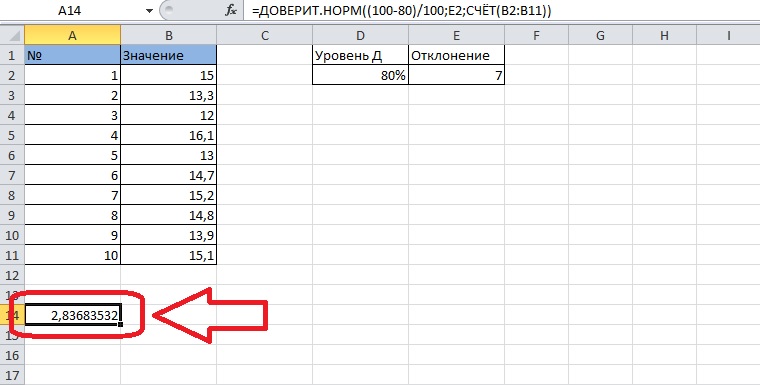8

Нормальное распределение

Когда известна вариация (σ 2) генеральной совокупности данных, для расчета доверительных пределов (граничных точек доверительного интервала) может быть использована z-оценка. По сравнению с применением t-распределения, использование z-оценки позволит построить не только более узкий доверительный интервал, но и получить более надежные оценки математического ожидания и среднеквадратического (стандартного) отклонения (σ), поскольку Z-оценка основывается на нормальном распределении.

Формула

Для определения граничных точек доверительного интервала, при условии что известно среднеквадратическое отклонение генеральной совокупности данных, используется следующая формула

L = X — Z α/2	σ
√n

Пример

Предположим, что размер выборки насчитывает 25 наблюдений, математическое ожидание выборки равняется 15, а среднеквадратическое отклонение генеральной совокупности составляет 8. Для уровня значимости α=5% Z-оценка равна Z α/2 =1,96. В этом случае нижняя и верхняя граница доверительного интервала составят

L = 15 — 1,96	8	= 11,864
√25

L = 15 + 1,96	8	= 18,136
√25

Таким образом, мы можем утверждать, что с вероятностью 95% математическое ожидание генеральной совокупности попадет в диапазон от 11,864 до 18,136.

Методы сужения доверительного интервала

Допустим, что диапазон является слишком широким для целей нашего исследования. Уменьшить диапазон доверительного интервала можно двумя способами.

1. Снизить уровень статистической значимости α.
2. Увеличить объем выборки.

Снизив уровень статистической значимости до α=10%, мы получим Z-оценку равную Z α/2 =1,64. В этом случае нижняя и верхняя граница интервала составят

L = 15 — 1,64	8	= 12,376
√25

L = 15 + 1,64	8	= 17,624
√25

А сам доверительный интервал может быть записан в виде

В этом случае, мы можем сделать предположение, что с вероятностью 90% математическое ожидание генеральной совокупности попадет в диапазон .

Если мы хотим не снижать уровень статистической значимости α, то единственной альтернативой остается увеличение объема выборки. Увеличив ее до 144 наблюдений, получим следующие значения доверительных пределов

L = 15 — 1,96	8	= 13,693
√144

L = 15 + 1,96	8	= 16,307
√144

Сам доверительный интервал станет иметь следующий вид

Таким образом, сужение доверительного интервала без снижения уровня статистической значимости возможно только лишь за счет увеличения объема выборки. Если увеличение объема выборки не представляется возможным, то сужение доверительного интервала может достигаться исключительно за счет снижения уровня статистической значимости.

Калькулятор доверительного интервала

Что такое доверительный интервал?

Простое определение доверительного интервала — это диапазон значений, включающий параметр генеральной совокупности. Значение этого параметра неизвестно. Когда дело доходит до лучшего варианта расчета, лучше всего использовать калькулятор доверительного интервала.

Формула доверительного интервала

Доверительный интервал можно рассчитать по следующей формуле:

\ (\ textbf {Значение нижней границы = Среднее значение (x) — Погрешность} \)

\ (\ textbf {Верхний Связанное значение = среднее значение (x) + предел погрешности} \)

Доверительный интервал зависит от стандартной ошибки и допустимой погрешности.Формула для стандартного отклонения может быть выражена как:

Стандартная ошибка \ (= \ dfrac {\ sigma} {\ sqrt {n}} \)

Формула для погрешности может быть записана как:

Предел погрешности ошибка \ (= \ text {стандартная ошибка} \ times \ text {Z} (0.95) \).

Где Z (0,95) представляет собой z-оценку, равную 95% доверительному уровню. Если вы используете определенный уровень достоверности, вместо этого фактора необходимо определить правильный z-показатель.

Как рассчитать доверительный интервал?

Здесь мы проиллюстрируем метод нахождения доверительного интервала с использованием приведенных выше формул.Выполните следующие шаги, чтобы вычислить доверительный интервал:

1. Определите и запишите значения
2. Вычислите стандартную ошибку, используя формулу стандартной ошибки
3. Вычислите предел погрешности, используя формулу предельной погрешности
4. Для вычисления верхней и нижней границы доверительного интервала, добавьте и вычтите погрешность из среднего значения.

Пример:

Как найти 95% доверительный интервал?

Давайте разберемся с порядком вычисления доверительного интервала на примере.

Предположим, что имеется выборка из 50 чаш разных размеров. Стандартное отклонение составляет 4 , а средний размер равен 10. Каким будет доверительный интервал?

Решение:

Мы рассчитаем доверительный интервал, используя приведенные выше формулы шаг за шагом. Выполните следующие шаги, чтобы получить доверительный интервал для данных значений:

Определите и запишите значения.

\ (\ sigma = 4, n = 50, \ Mu = 10 \)

Рассчитайте стандартную ошибку, используя уравнение стандартной ошибки.

Стандартная ошибка \ (= \ dfrac {\ sigma} {\ sqrt {n}} = \ dfrac {4} {\ sqrt {50}} = 0,56 \)

Рассчитайте предел погрешности с использованием уравнения погрешности. Предел погрешности будет определяться на основе вычисленного выше стандартного значения ошибки.

Предел погрешности \ (= \ text {Стандартная ошибка} \ times Z (0,95) \)

Здесь член \ (Z (0,95) \) определяет значение Z-оценки при доверительном интервале 95%. ,Обратитесь к этой таблице Z, чтобы получить значение Z. В этом случае \ (Z = 1.758 \).

Предел погрешности \ (= 0,56 \ раз 1,758 = 0,98 \)

Теперь, чтобы вычислить верхнюю и нижнюю границы доверительного интервала, сложите и вычтите предел погрешности из среднее значение.

Среднее значение = 10

Следовательно, диапазон будет записан как:

\ (10 ​​- 0,98 \ leftrightarrow 10 + 0,98 \)

Итак,

Нижняя граница \ (= 9.02 \)

Верхняя граница \ (= 10.98 \)

Как пользоваться нашим калькулятором доверительного интервала?

Чтобы использовать наш калькулятор доверительного интервала:

• Выберите значение из исходных данных или Среднее и стандартное отклонение.
• Выберите уровень достоверности из списка. 95 Уровень достоверности будет выбран по умолчанию, если вы не выберете уровень достоверности.
• Введите среднее значение и значение стандартного отклонения в указанные поля ввода.
• Введите размер выборки в данное поле ввода.
• Нажмите кнопку Рассчитать , чтобы увидеть результат.

Калькулятор доверительного интервала мгновенно вычислит доверительный интервал с выбранным уровнем достоверности и покажет вам доверительный интервал, а также допустимую погрешность. Вы можете использовать наш калькулятор стандартного отклонения, чтобы рассчитать стандартное отклонение для доверительного интервала.

Часто задаваемые вопросы

Что означает 95% доверительный интервал?

Уровень достоверности 95% означает, что в 95% случаев результаты будут представлять результаты для всей популяции, если исследование или эксперимент были воспроизведены.Иногда из-за времени или затрат невозможно опросить всех.

Что такое хороший доверительный интервал?

Ваша статистическая точность зависит от изменчивости и размера выборки. Низкая изменчивость или больший размер выборки соответствуют более узкому доверительному интервалу с более низкой погрешностью. Более высокая вариабельность или меньший размер выборки могут привести к большему доверительному интервалу с

Точечная оценка

Как известно из , статистика
(обозначим ее Х ср
) является несмещенной оценкой среднего
этой генеральной совокупности
и имеет распределение N(μ;σ 2 /n).

Примечание
Что делать, если требуется построить доверительный интервал
в случае распределения, которое не является
нормальным?
В этом случае на помощь приходит , которая гласит, что при достаточно большом размере выборки
n из распределения не являющемся
нормальным
, выборочное распределение статистики Х ср
будет приблизительно
соответствовать нормальному распределению
с параметрами N(μ;σ 2 /n).

Итак, точечная оценка
среднего
значения распределения
у нас есть – это среднее значение выборки
, т.е. Х ср
. Теперь займемся доверительным интервалом.

Как построить доверительный интервал в excel

В этой статье описаны синтаксис формулы и использование в Microsoft Excel.

Описание

Возвращает доверительный интервал для среднего генеральной совокупности с нормальным распределением.

Доверительный интервал — это диапазон значений. Выборка «x» находится в центре этого диапазона, а диапазон — x ± ДОВЕРИТ. Например, если x — это пример времени доставки продуктов, заказаных по почте, то x ± ДОВЕРИТ — это диапазон средств численности населения. Для любого средней численности населения (μ0) в этом диапазоне вероятность получения выборки от μ0 больше, чем x, больше, чем альфа; для любого средней численности населения (μ0, не в этом диапазоне), вероятность получения выборки от μ0 больше, чем x, меньше, чем альфа. Другими словами, предположим, что для построения двунамерного теста на уровне значимости альфа гипотезы о том, что это μ0, используются значения x, standard_dev и размер. Тогда мы не отклонить эту гипотезу, если μ0 находится через доверительный интервал, и отклонить эту гипотезу, если μ0 не находится в доверительный интервал. Доверительный интервал не позволяет нам сделать вывод о том, что вероятность 1 — альфа, что следующий пакет займет время доставки через доверительный интервал.

Важно: Эта функция была заменена одной или несколькими новыми функциями, которые обеспечивают более высокую точность и имеют имена, лучше отражающие их назначение. Хотя эта функция все еще используется для обеспечения обратной совместимости, она может стать недоступной в последующих версиях Excel, поэтому мы рекомендуем использовать новые функции

Чтобы узнать больше о новых функциях, см. в разделах Функция ДОВЕРИТ.НОРМ и Функция ДОВЕРИТ.СТЬЮДЕНТ.

Синтаксис

Аргументы функции ДОВЕРИТ описаны ниже.

Альфа — обязательный аргумент. Уровень значимости, используемый для вычисления доверительного уровня. Доверительный уровень равен 100*(1 — альфа) процентам или, иными словами, значение аргумента «альфа», равное 0,05, означает 95-процентный доверительный уровень.

Стандартное_откл — обязательный аргумент. Стандартное отклонение генеральной совокупности для диапазона данных, предполагается известным.

Размер — обязательный аргумент. Размер выборки.

Замечания

Если какой-либо из аргументов не является числом, возвращается #VALUE! значение ошибки #ЗНАЧ!.

Если альфа ≤ 0 или ≥ 1, доверит возвращает #NUM! значение ошибки #ЗНАЧ!.

Если Standard_dev ≤ 0, возвращается #NUM! значение ошибки #ЗНАЧ!.

Если значение аргумента «размер» не является целым числом, оно усекается.

Если размер < 1, доверит возвращает #NUM! значение ошибки #ЗНАЧ!.

Если предположить, что альфа = 0,05, то нужно вычислить область под стандартной нормальной кривой, которая равна (1 — альфа), или 95 процентам. Это значение равно ± 1,96. Следовательно, доверительный интервал определяется по формуле:

Пример

Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.

Выбор варианта отображения процента в ячейке

Как ранее уже было сказано, проценты могут выглядеть в виде обычных чисел со знаком %, либо в виде десятичных дробей. В Excel можно выбрать оба варианта отображения ячеек.

Для этого, правой кнопкой мыши щелкните на ячейку с процентным значением, далее выберите пункт “Формат ячеек”.

В открывшемся окне в разделе “Число” можно выбрать “Процентный” формат отображения ячейки и сразу посмотреть образец, как это будет выглядеть.

Также, в этом же разделе можно выбрать “Числовой” формат, при котором проценты будут отображаться в виде десятичных дробей, а само значение процента автоматически будет пересчитано (т.е. вместо 15% будет отображаться 0,15).

Надеемся, данное руководство будет полезно при вычислениях с процентными величинами в Microsoft Excel, как новичку, так и опытному пользователю.

Как самостоятельно рассчитать доверительный интервал в Excel?

Расчет доверительного интервала в Excel (т.е. верхней и нижней границы прогноза) рассмотрим на примере. У нас есть временной ряд — продажи по месяцам за 5 лет. См. Вложенный файл.

Для расчета границ прогноза рассчитаем:

1. Прогноз продаж (см. статью «Как самостоятельно рассчитать прогноз продаж с учетом роста и сезонностью»).
2. Сигма — среднеквадратическое отклонение модели прогноза от фактических значений.
3. Три сигма.
4. Доверительный интервал.

1. Прогноз продаж.

О том, «как рассчитать прогноз продаж с учетом роста и с сезонностью» подробно описано в данной статье. Поэтому для тех, кто еще не изучал данный материал и не знает, как самостоятельно рассчитать прогноз продаж по месяцам с учетом роста и сезонности, рекомендуем для понимания последующих действий изучить данную статью, а затем перейти к дальнейшему изучению данного материала.

Для расчета сигма рассчитаем среднеквадратическое отклонение для каждого месяца.

1. Для этого на 7-м шаге во вложенном файле рассчитаем значения прогнозной модели, в нашем случае это прогноз с линейным трендом и сезонностью.

Значение модели = Значение тренда умножим на коэффициент сезонности соответствующего месяца.

В Excel введем формулу:

=RC (ссылка на тренд)*ВПР(RC;R8C9:R19C10;2;0)(формула ВПР со ссылкой на коэффициент сезонности соответствующего месяца)

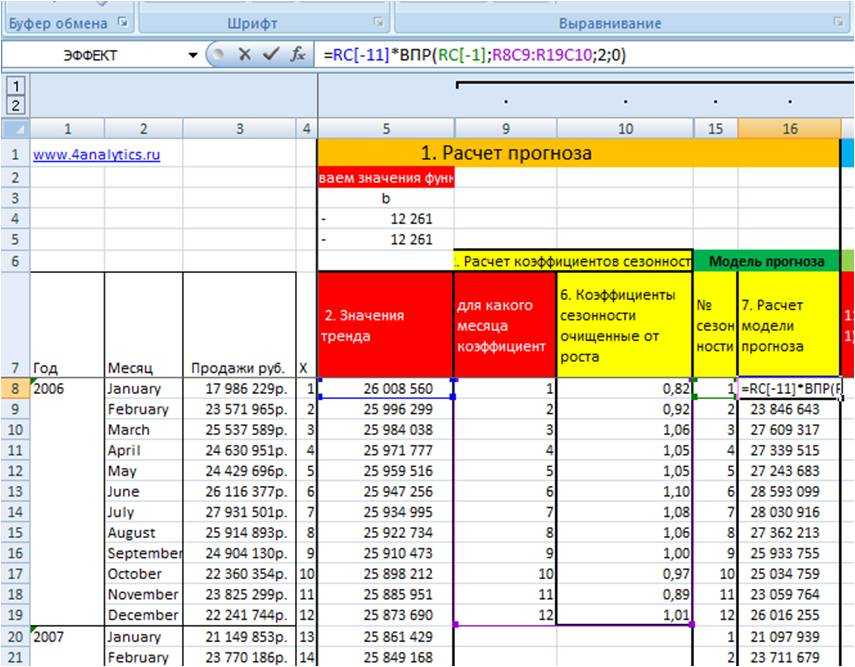
2. Рассчитаем квадрат разницы фактических значений и прогнозной модели (Xi-Ximod)^2 (8 этап во вложенном файле)

=(RC(данные во временном ряду) — RC(значение модели))^2(в квадрате)

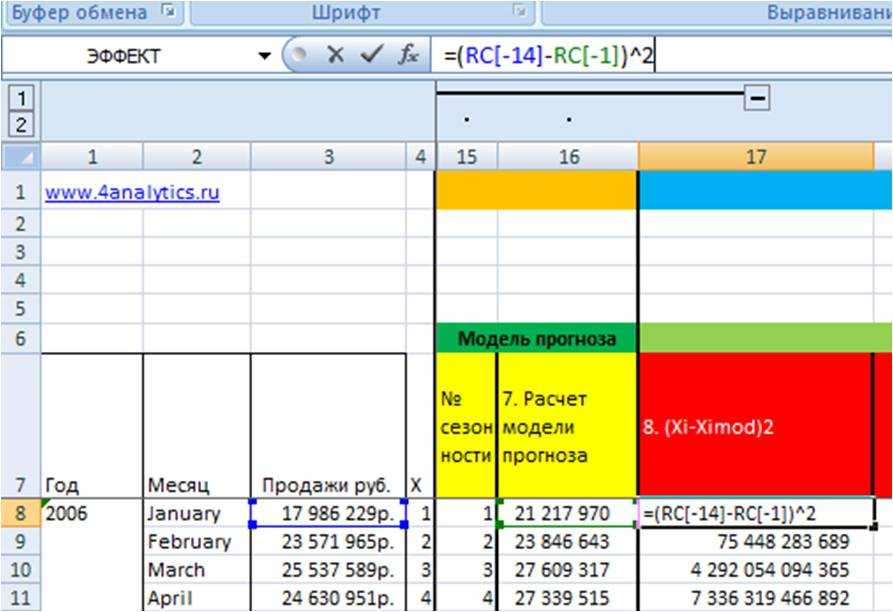
3. Просуммируем для каждого месяца значения отклонений из 8 этапа Сумма((Xi-Ximod)^2), т.е. просуммируем январи, феврали… для каждого года.

Для этого воспользуемся формулой =СУММЕСЛИ()

=СУММЕСЛИ(массив с номерами периодов внутри цикла (для месяцев от 1 до 12);ссылка на номер периода в цикле; ссылка на массив с квадратами разницы исходных данных и значений периодов)

(9 этапво вложенном файле)

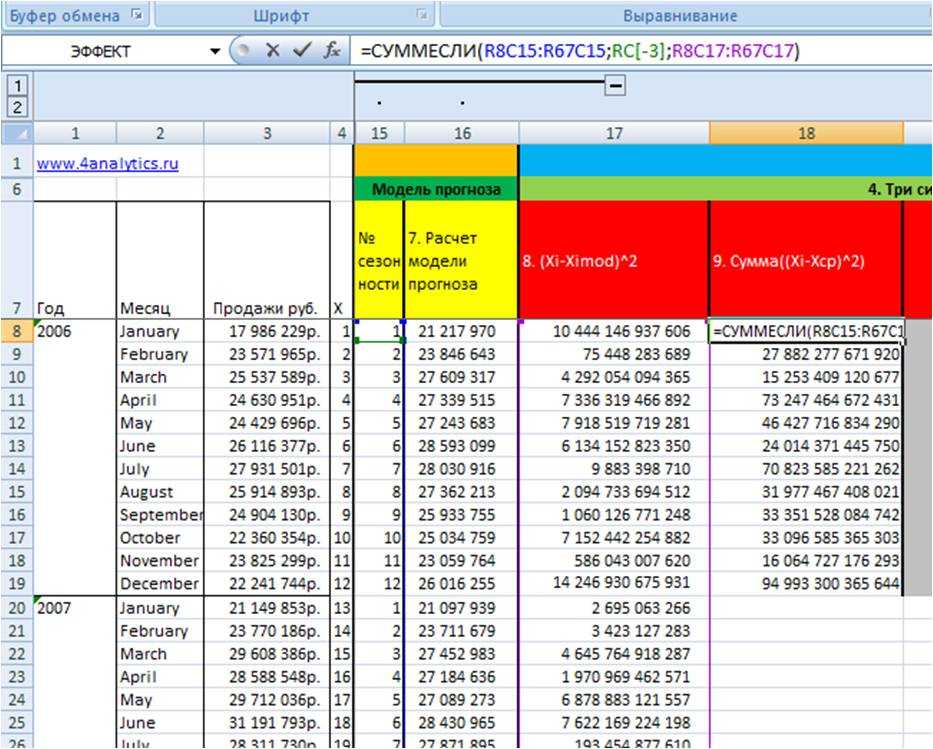
4. Рассчитаем среднеквадратическое отклонение для каждого периода в цикле от 1 до 12 (10 этапво вложенном файле).

Для этого из значения рассчитанного на 9 этапе мы извлекаем корень и делим на количество периодов в этом цикле минус 1 = КОРЕНЬ((Сумма(Xi-Ximod)^2/(n-1))

Воспользуемся формулами в Excel =КОРЕНЬ(R8 (ссылка на (Сумма(Xi-Ximod)^2)/(СЧЁТЕСЛИ($O$8:$O$67 (ссылка на массив с номерами цикла); O8 (ссылка на конкретный номер цикла, которые считаем в массиве))-1))

С помощью формулы Excel = СЧЁТЕСЛИ мы считаем количество n

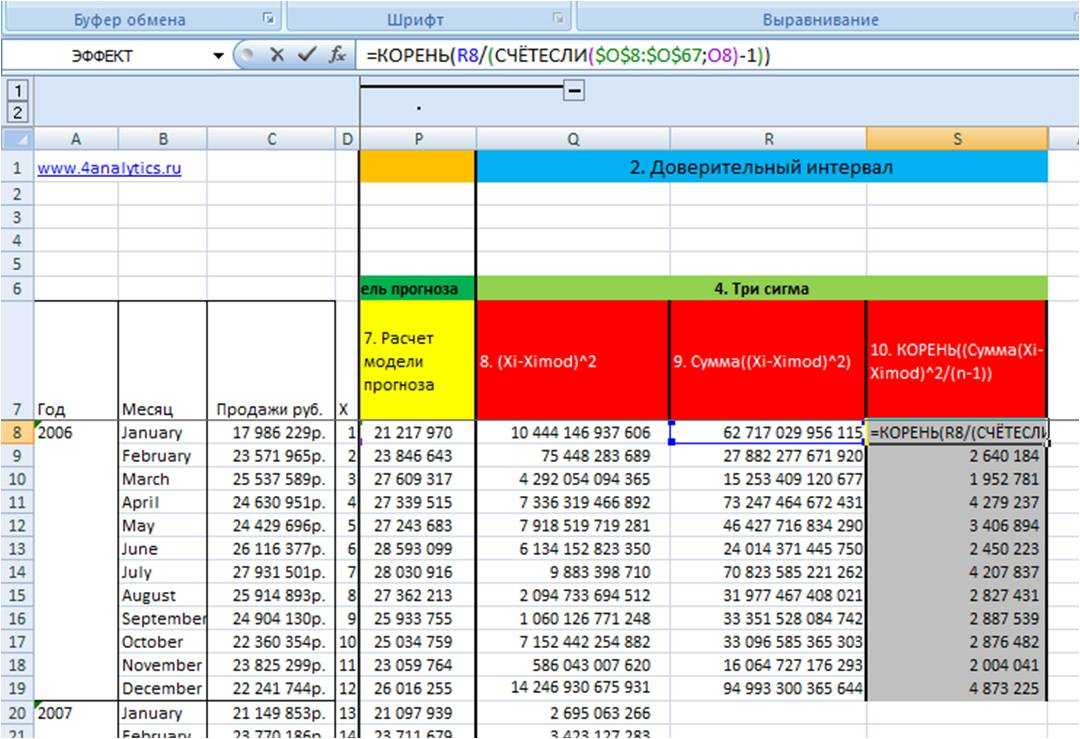
Рассчитав среднеквадратическое отклонение фактических данных от модели прогноза, мы получили значение сигма для каждого месяца — этап 10 во вложенном файле.

На 11 этапе задаем количество сигм — в нашем примере «3» (11 этапво вложенном файле):

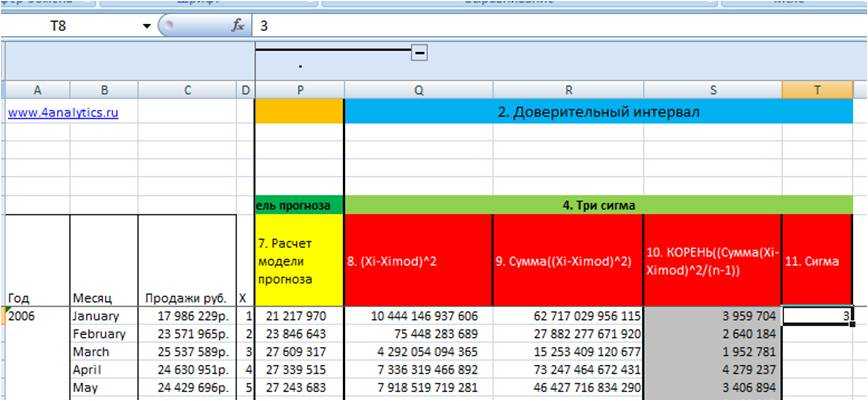
Также удобные для практики значения сигма:

1,64 сигма — 10% вероятность выхода за предел (1 шанс из 10);

1,96 сигма — 5% вероятность выхода за пределы (1 шанс из 20);

2,6 сигма — 1% вероятность выхода за пределы (1 шанс из 100).

5) Рассчитываем три сигма, для этого мы значения «сигма» для каждого месяца умножаем на «3».

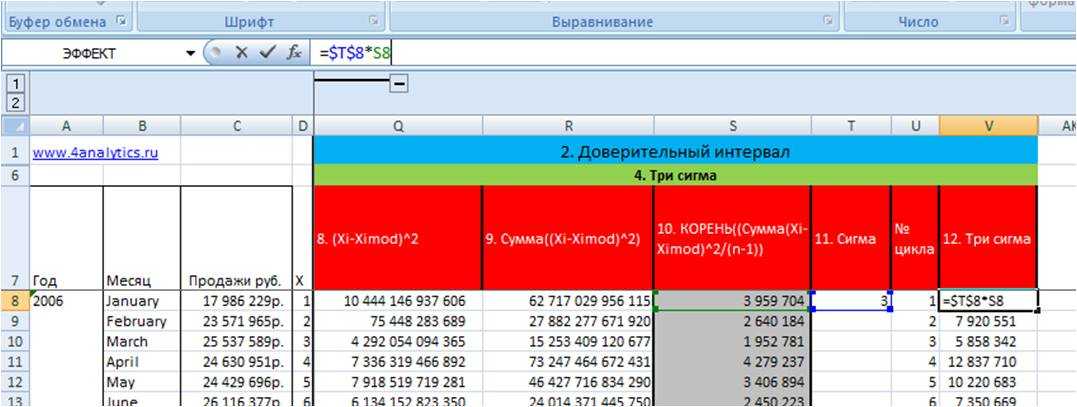
3.Определяем доверительный интервал.

1. Верхняя граница прогноза — прогноз продаж с учетом роста и сезонности + (плюс) 3 сигма;
2. Нижняя граница прогноза — прогноз продаж с учетом роста и сезонности – (минус) 3 сигма;

Для удобства расчета доверительного интервала на длительный период (см. вложенный файл) воспользуемся формулой Excel =Y8+ВПР(W8;$U$8:$V$19;2;0), где

Y8 — прогноз продаж;

W8 — номер месяца, для которого будем брать значение 3-х сигма;

$U$8:$V$19 — таблица, из которой с помощью функции =ВПР извлекаем значение 3-х сигма, соответствующее данному месяцу, фиксируем ссылку на таблицу с помощью F4, подробнее в статье «Как зафиксировать ссылку в Excel».

Т.е. Верхняя граница прогноза = «прогноз продаж» + «3 сигма» (в примере, ВПР(номер месяца; таблица со значениями 3-х сигма; столбец, из которого извлекаем значение сигма равное номеру месяца в соответствующей строке;0)).

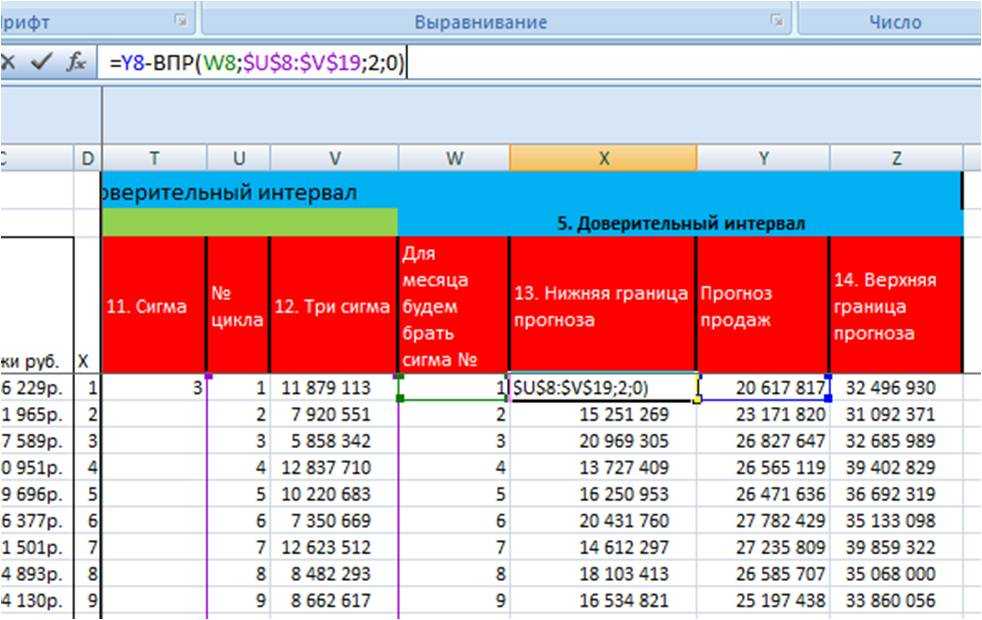
Нижняя граница прогноза = «прогноз продаж» минус «3 сигма».

Итак, мы рассчитали доверительный интервал в Excel.

Теперь у нас есть прогноз и диапазон с границами в пределах, которого с заданной вероятностью сигма попадут фактические значения.

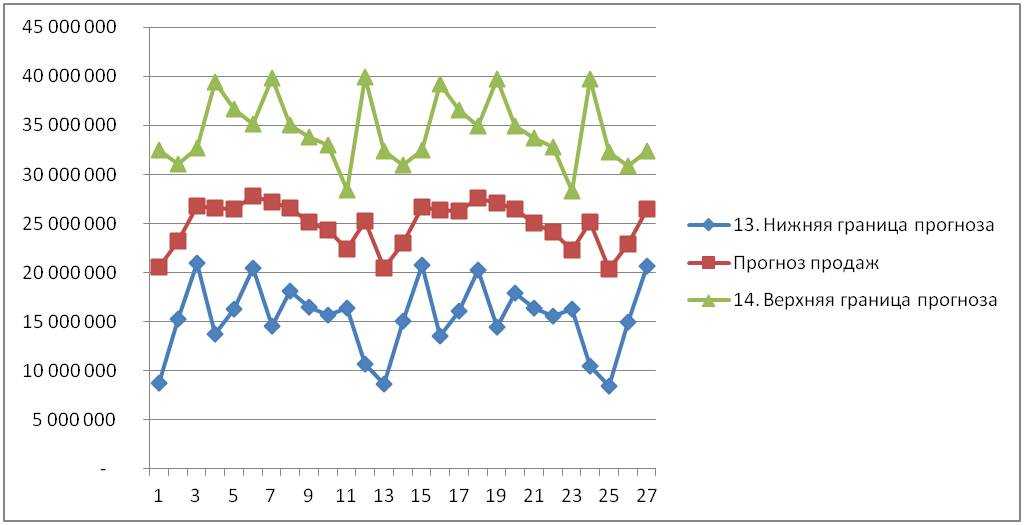
В данной статье мы рассмотрели, что такое сигма и правило трёх сигм, как определить доверительный интервал и для чего вы можете использовать данную методику на практике.