Формула для расчета аннуитетного платежа в excel

Преимущества использования аннуитетных платежей

Использование аннуитетных платежей имеет следующие преимущества:

1. Постоянные платежи: Аннуитетные платежи представляют собой фиксированные суммы, которые не меняются в течение всего срока кредита. Такой подход позволяет заемщику лучше планировать свои финансы и предсказать расходы на погашение кредита.

2. Простота расчетов: Формула расчета аннуитетных платежей относительно проста и легко применима в программе Excel. Нет необходимости в сложных математических расчетах, что упрощает процесс планирования и контроля выплат.

3. Удобство: Аннуитетные платежи обеспечивают простоту и удобство ведения финансовых операций. Заемщику не нужно запоминать разные суммы и даты платежей, он просто выплачивает одинаковую сумму каждый месяц.

4. Меньшие процентные расходы: Аннуитетные платежи позволяют заемщику минимизировать свои процентные расходы на долг. В начале срока кредита основной долг относительно невелик, и проценты составляют большую часть платежа. Со временем сумма основного долга увеличивается, и проценты уменьшаются, что позволяет заемщику экономить на процентах.

5. Условия возврата: Использование аннуитетных платежей позволяет заемщику гибко подходить к выбору срока погашения кредита. Он может выбрать более короткий или более длительный срок в зависимости от своих финансовых возможностей и потребностей.

В целом, аннуитетные платежи предлагают преимущества, такие как предсказуемость, удобство и экономию процентов, что делает их привлекательным выбором для заемщиков при погашении кредитов.

Кредитный калькулятор для расчёта простых кредитов

Начнём с простого варианта, быстро прикинем, сколько нам нужно ежемесячно оплачивать по аннуитетному кредиту, это когда выплаты делают одинаковыми суммами, как в большинстве случаев. Это можно произвести одной функцией Excel и несколькими простыми формулами. Для получения результата в Excel существует функция ПЛТ в разделе «Финансовые». Указываем, в какую ячейку нужен результат, вызываем «Мастер функций» ищем функцию ПЛТ, нажимаем кнопочку «ОК» и в окне мастера вводим необходимые аргументы для нашего расчёта, формула получается следующего вида:

=ПЛТ(B5/12;B6;B4;0;0), где:

• Ставка (B5/12) – является аргументом, указывающим на процентную ставку по взятому кредиту в разрезе периодов выплат, в нашем случае это месяцы. Если ставка по кредиту в год 18%, то за один месяц будет составлять 1,5%;
• Кпер (B6) – аргумент, указывающий на количество периодов, то есть, на сколько месяцев взят кредит;
• Бс (B4) – указываем, какую сумму кредита будем рассчитывать;
• Пс (0) – это финишная пряма, какой итог кредита должен быть в конце, скорее всего это будет 0, что означает, что вы никому и ничего не должны;
• Тип (0) – аргумент необходимый для учёта выплат каждый месяц. Если равно 1 – это учитываем выплаты к началу месяца, если 0 – то учитываем на конец. В постсоветском пространстве большинство банков используют последний вариант, а значит вводим 0.

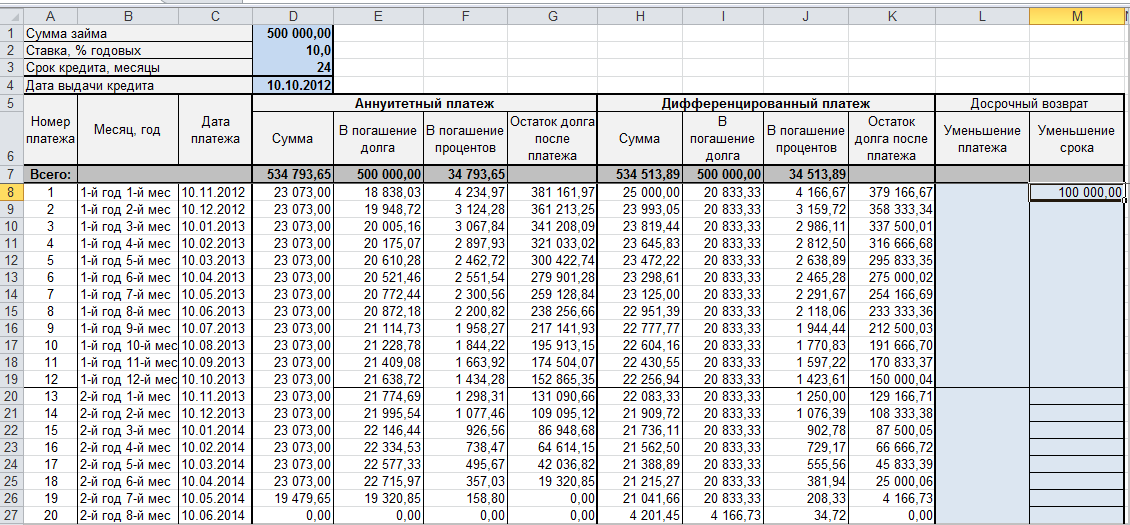
Кроме этого, необходимо рассчитать, сколько составит общая сумма выплаты, и какая переплата получится, когда вы вернёте деньги банку. Это легко осуществить при помощи простых формул. Теперь давайте немного улучшим и детализируем наш отчёт с помощью функции ОСПЛТ, которая определяет часть основного платежа по телу кредита и функции ПРПЛТ, которая посчитает всё, что касается процентов банку за использование кредита. Видоизменим ваш расчёт следующей таблицей:

Теперь в поле «Тело кредита» в ячейку Е2 вводим формулу функции ОСПЛТ следующего вида:

=ОСПЛТ($B$4/12;D2;$B$5;$B$3;0)

Как видите, ее орфография практически аналогична функции ПЛТ, добавился только аргумент «Период», который указывает на номер текущего месяца, и дополнительно рассматривать ее я не буду

Единственное, на что обращу ваше внимание, это то, что формула будет растянута на диапазон, а значит, аргументы необходимо закрепить абсолютными ссылками. Следующим шагом для столбика «Проценты» будем использовать возможности функции ПРПЛТ

Вводится она аналогично вышеописанной и с теми же условиями и будет иметь такой вид:

=ПРПЛТ($B$4/12;D2;$B$5;$B$3;0) Теперь в оставшиеся столбики будем вводить простые формулы, для получения суммы выплаты нам нужна формула: =E2+F2, а для определения суммы остатка кредита используем формулу: =$B$3+СУММ($E$2:E2). При необходимости, возможно, немножко улучшить и автоматизировать ваш кредитный калькулятор в Excel для уменьшения количества ошибок.

Для начала пропишем формулу в ячейку D3 для того чтобы она подстраивала и отслеживала срок кредита:

=ЕСЛИ(D2>=$B$5;»«;D2+1)

Следующим шагом с помощью логической функции ЕСЛИ для поля «Тело кредита», сделаем автоматическую проверку достигли ли вы последнего срока выплат или нет. Если период, достигнут, получаем пустую ячейку «», а если нет, то функцией ОСПЛТ выводим необходимый расчёт:

=ЕСЛИ(D3<>»»;ОСПЛТ($B$4/12;D3;$B$5;$B$3;0);»»)

Как рассчитать долг на конец месяца в графике аннуитетных платежей

Прежде всего, надо понимать, что именно является вашим долгом по кредиту, и какие выплаты способствуют его уменьшению. В нашем примере вы берёте в кредит 50 000 рублей – это и есть ваш долг. Переплаченные по кредиту проценты (6157 рублей) вашим долгом не являются, это всего лишь вознаграждение банку за предоставленный кредит. Таким образом, можно сделать вывод:

Погашение процентов по кредиту никак не способствует уменьшению вашего долга перед банком.

В кризисные времена банки часто «идут навстречу» своим должникам. Они говорят как-то так: «Мы понимаем, у вас сейчас проблемы! Окей, наш банк готов пойти вам на уступки – можете нам просто погашать проценты, а само тело кредита погашать не надо. Все же люди братья и должны друг другу помогать! Бла-бла-бла…»

На первый взгляд такое предложение может показаться выгодным, а сам банк – «белым и пушистым лапулей». Ага, как бы ни так! Если взять в руки калькулятор и провести простые арифметические расчёты, то сразу становится ясно, что реальное предложение банка выглядит приблизительно так:

«Ребята, вы попали на деньги! Ничего не поделаешь, это жизнь! Предлагаем вам на время (а может и навсегда) стать нашим рабом – будете ежемесячно выплачивать проценты по кредиту, а сам долг погашать не надо (ну, чтобы сумма выплат по процентам не уменьшалась). Ничего личного – это просто бизнес, друзья!»

Теперь запомните главную мысль:

Именно погашение тела кредита вытаскивает вас из долговой ямы. Не процентов, а именно тела кредита.

Наверняка вы уже догадались, как рассчитывается долг на конец месяца в нашем графике платежей. В общем, формула выглядит так:

Sn2 – долг на конец месяца по аннуитетному кредиту; Sn1 – сумма текущей задолженности по кредиту; S – сумма в аннуитетном платеже, которая идёт на погашение тела кредита.

Обратите внимание! При расчёте долга на конец месяца, от общей суммы текущей задолженности отнимается только та часть платежа, которая идёт на погашение тела кредита (уплаченные проценты сюда не входят). Давайте для наглядности посчитаем, каким будет долг на конец месяца по нашему кредиту после внесения первого платежа:. Давайте для наглядности посчитаем, каким будет долг на конец месяца по нашему кредиту после внесения первого платежа:

Давайте для наглядности посчитаем, каким будет долг на конец месяца по нашему кредиту после внесения первого платежа:

Итак, при первом платеже текущая задолженность по кредиту у нас равна всей сумме займа (50 000 руб.). Чтобы посчитать долг на конец месяца, мы отнимаем от этой суммы не весь ежемесячный платёж (4680 руб.), а только ту часть, которая ушла на погашение тела кредита (3763 руб.). В результате наш долг на конец месяца составит 46 237 руб., именно на эту сумму будут начисляться проценты в следующем месяце. Естественно, они будут меньше, так как сумма долга уменьшилась

Теперь вы понимаете, почему важно погашать именно тело кредита?

Итак, друзья, мы с вами разобрались с формулами и расчетами аннуитетных платежей. Надеемся, теперь у вас нет вопросов по этой теме, и вы запросто сможете произвести все необходимые расчеты, а также составить график аннуитетных платежей по кредиту. Единственное, что бы вам, наверное, хотелось, это как-то автоматизировать процесс расчетов. Вы не поверите, но это возможно! Хотите узнать как? Тогда переходим к публикации: Расчет аннуитетных платежей по кредиту в Excel.

⇧

Досрочное погашение аннуитетного кредита

Всего есть два вариант досрочных выплат. Аннуитетный калькулятор рассчитан и на такие варианты погашения, поэтому достаточно просто знать, по каким сценариям могут развиваться события при необходимости отдать займ раньше срока. В банковском отделении Вам предложат такие варианты:

• Сократить период выплат в аннуитетной системе. Так, понадобится совершить дополнительный платёж. При этом месячная ставка не возрастёт. Платёж будет представлять собой компенсацию банку в размере процентов, которые он не получит.
• Уменьшение ежемесячных выплат. В этом случае уменьшается аннуитетная ставка, но размер процента не меняется (допустимо только при условии сокращения выплат по основной задолженности).

Такая возможность погашения аннуитета есть не везде. Даже включая, наш кредитный калькулятор. Скоро мы обязательно внесем в него правки и добавим эту возможность.  Поэтому, рекомендуем произвести расчёт аннуитетных платежей по кредиту на калькуляторе с каждым досрочным погашением, если Вы всё же решили перейти к ежемесячному уменьшению выплат, а не к сокращению срока кредитования.

Это интересно: Расчет годовых процентов по кредиту — формула

Примеры расчетов регулярных платежей по аннуитетной схеме в Excel

Функция ОСПЛТ используется для расчетов задолженностей по аннуитетной схеме. То есть, сумма платежа за каждый период состоит из тела кредита (основной суммы задолженности) и процентов (части средств, которые выплачивают сверху за использование финансового продукта). Процентная ставка является неизменной величиной. Соотношение процентной части к телу кредита в каждом периодическом платеже меняется со временем. Рассматриваемая функция позволяет определить сумму основной задолженности (без учета процентов), выплаченной в определенный период согласно графику.

Пример 1. Банк выдал кредит на сумму 10 000 руб. под 18% годовых сроком на 1 год. Был составлен график ежемесячных выплат. Определить, какую сумму тела кредита выплатит клиент в 3-1 месяц.

Вид таблицы данных:

Для расчета используем следующую функцию:

=ОСПЛТ(B3/12;3;B4;B5)

Описание аргументов:

• B3/12 – размер ставки, приведенной к числу периодов выплат (12 месяцев);
• 3 – номер периода, для которого выполняется расчет;
• B4 – общее число периодов (12 месяцев в году);
• B5 – сумма кредита по договору.

Результат вычислений:

Полученное значение – отрицательное число, поскольку оно отражает расходы клиента по оплате финансового продукта.

Основная формула аннуитетного платежа в Excel

Как и говорилось выше, в Microsoft Office Excel можно работать с различными типами платежей по кредитам и ссудам. Аннуитет не является исключением. В общем виде формула, с помощью которой можно быстро вычислить аннуитетные взносы, выглядит следующим образом:  

Основные значения формулы расшифровываются так:

• АП – аннуитетный платеж (название сокращено).
• О – размер основного долга заемщика.
• ПС – процентная ставка, выдвигаемая ежемесячно конкретным банком.
• С – число месяцев, на протяжении которых длится кредитование.

Для усвоения информации достаточно привести несколько примеров использования данной формулы. О них пойдет речь далее.

Примеры использования функции ПЛТ в Excel

Приведем простое условие задачи. Необходимо посчитать ежемесячный кредитный платеж, если банк выдвигает процент в размере 23%, а общая сумма составляет 25000 рублей. Кредитование продлится на протяжении 3-х лет. Задача решается по алгоритму:

1. Составить общую таблицу в Excel по исходным данным.

Таблица, составленная по условию задачи. В действительности можно задействовать другие столбцы для ее размещения

2. Активировать функцию ПЛТ и ввести для нее аргументы в соответствующее окошко.
3. В поле «Ставка» прописать формулу «В3/В5». Это и будет процентная ставка по взятому кредиту.
4. В строке «Кпер» написать значение в виде «В4*В5». Это будет общее количество выплат за весь срок кредитования.
5. Заполнить поле «Пс». Здесь нужно указать первоначальную сумму, взятую в банке, прописав значение «В2».

Необходимые действия в окне «Аргументы функции». Здесь указан порядок заполнения каждого параметра

6. Удостовериться, что после нажать «ОК» в исходной таблице посчиталось значение «Ежемесячный платеж».

Финальный результат. Ежемесячный платёж посчитан и выделен красным цветом

Пример расчета суммы переплаты по кредиту в Excel

В этой задаче надо подсчитать сумму, которую переплатит человек, взявший кредит 50000 рублей по процентной ставке 27% на 5 лет. Всего в год заемщик производит 12 выплат. Решение:

1. Составить исходную таблицу данных.

Таблица, составленная по условию задачи

2. Из общей суммы выплат отнять первоначальный размер суммы по формуле «=ABS(ПЛТ(B3/B5;B4*B5;B2)*B4*B5)-B2». Ее надо вставить в строку формул сверху главного меню программы.
3. В итоге в последней строке созданной таблички появится сумма переплат. Заемщик переплатит 41606 рублей сверху.

Финальный результат. Практически двукратная переплата

Формула вычисления оптимального ежемесячного платежа по кредиту в Excel

Задача с таким условием: клиент зарегистрировал счет в банке на 200000 рублей с возможностью ежемесячного пополнения. Нужно посчитать количество платежа, который человек должен вносить каждый месяц, чтобы через 4 года на его счету оказалось 2000000 рублей. Ставка составляет 11%. Решение:

1. Составить табличку по исходным данным.

Таблица, составленная по данным из условия задачи

2. В строку ввода Эксель ввести формулу «=ПЛТ(B3/B5;B6*B5;-B2;B4)» и нажать «Enter» с клавиатуры. Буквы будут отличаться в зависимости от ячеек, в которых размещена таблица.
3. Проверить, что сумма взноса автоматически посчиталась в последней строке таблицы.

Окончательный результат расчета

Особенности использования функции ПЛТ в Excel

В общем виде данная формула записывается следующим образом: =ПЛТ(ставка; кпер; пс; ; ). У функции есть следующие особенности:

Когда рассчитываются ежемесячные взносы, в рассмотрение берется исключительно годовая ставка.
Указывая размер процентной ставки, важно сделать перерасчет, опираясь на число взносов за год.
Вместо аргумента «Кпер» в формуле указывается конкретное число. Это период выплат по задолженности.

Аннуитет. Определяем процентную ставку в EXCEL

Пусть известна сумма и срок кредита, а также величина регулярного аннуитетного платежа. Рассчитаем в MS EXCEL под какую процентную ставку нужно взять этот кредит, чтобы полностью его погасить за заданный срок. Также в статье разберем случай накопления вклада.

Для расчета процентной ставки в аннуитетной схеме используется функция СТАВКА() .

Функция СТАВКА(кпер; плт; пс; ; ; ) возвращает процентную ставку по аннуитету.

Примечание . Английский вариант функции: RATE(nper, pmt, pv, , , ), т.е. Number of Periods – число периодов.

Вот что написано на сайте MS : Ставка вычисляется путем итерации и может давать нулевое значение или несколько значений. Если последовательные результаты функции СТАВКА не сходятся с точностью 0,0000001 после 20-ти итераций, то СТАВКА возвращает сообщение об ошибке #ЧИСЛО! Попробуем разобраться причем здесь итерации. Взглянем на Формулу 1 (подробнее см. обзорную статью о функциях аннуитета ).

Если постараться решить это уравнение относительно параметра Ставка, то мы получим степенное уравнение (степень уравнения и, соответственно, число его корней будет зависеть от значения Кпер). В отличие от других параметров ПЛТ, БС, ПС и Кпер, найти универсальное решение этого уравнения для всевозможных степеней невозможно, поэтому приходится использовать метод итераций (по сути, метод подбора ). Чтобы облегчить поиск Ставки методом итераций, используется аргумент Предположение. Предположение — это приблизительное значение Ставки, т.е. прогноз на основании нашего знания о задаче. Если значение предположения опущено, то оно полагается равным 10 процентам. Значение Предположение также полезно в случае , если имеется несколько решений уравнения – в этом случае находится значение Ставки ближайшее к Предположению .

Задача1 – Выплата кредита

Определим под какую годовую ставку мы можем взять 100 000 руб., выплачивая ежемесячно 3000 руб. в течение 5 лет.

Примечание . Аннуитетная схема погашения кредита подробно рассмотрена в статье Аннуитет. Расчет периодического платежа в MS EXCEL. Погашение ссуды (кредита, займа) .

В условии задачи содержится следующая информация:

• Заемщик должен сделать 60 равновеликих платежей (12 мес. в году*5 лет), т.е. всего 60 периодов (Кпер);
• Проценты начисляются в конце каждого периода (если не сказано обратное, то подразумевается именно это), т.е. аргумент Тип=0;
• В конце срока задолженность должна быть равна 0 (БС=0).

В результате формула для вычисления годовой ставки будет выглядеть так =12*СТАВКА(12*5;-3000;100000;0;0) или =12*СТАВКА(12*5;-3000;100000) Знак минус у регулярного платежа показывает, что мы имеем разнонаправленные денежные потоки: +100000 – это деньги, которые банк дал нам, -3000 – это деньги, которые мы возвращаем банку . Результат вычисления = 26,10%

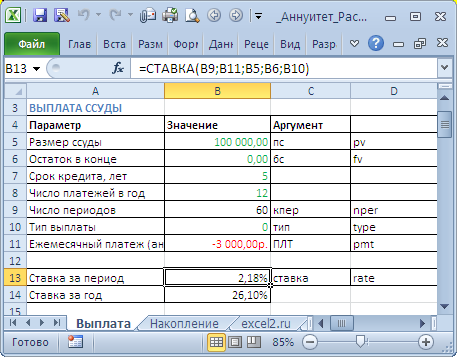
Формула может вернуть отрицательные значения ставки. Это происходит, когда сумма всех регулярных платежей недостаточна для погашения кредита даже при 0 ставке. Но, в нашем случае все в порядке: 60*(3000)=180000>100000. Отрицательная ставка означает, что банк выплачивает нам проценты за пользование кредитом, что является абсурдом. Это, конечно, ошибка (попробуйте например, в файле примера на Листе Выплата установить платеж =-1000).

Если задать платеж = 0 или того же знака, что и сумма кредита, то функция СТАВКА() вернет ошибку #ЧИСЛО! Это и понятно, при нулевых платежах погасить кредит невозможно.

Примечание . С помощью Подбора параметра можно найти величину регулярного платежа, который бы обеспечил выплату кредита при заданной процентной ставке (обратная задача). Но, по большому счету, в этом нет необходимости – для этого существует функция ПЛТ() .

Задача2 – Накопление суммы вклада

Определим, с какой годовой ставкой мы можем накопить 1 000 000 руб., внося ежемесячно по 10 000 руб. в течение 5 лет. (см. файл примера на Лист Накопление )

Примечание . Аннуитетная схема накопления целевой суммы подробно рассмотрена в статье Аннуитет. Расчет периодического платежа в MS EXCEL. Срочный вклад .

Формула для вычисления годовой ставки будет выглядеть так =12*СТАВКА(12*5;-10000;0;1000000) =19,38%

Здесь ПС=0, т.е. начальная сумма вклада =0 ( Приведенная Стоимость ). Целевой вклад = 1000000 (БС – Будущая Стоимость ).

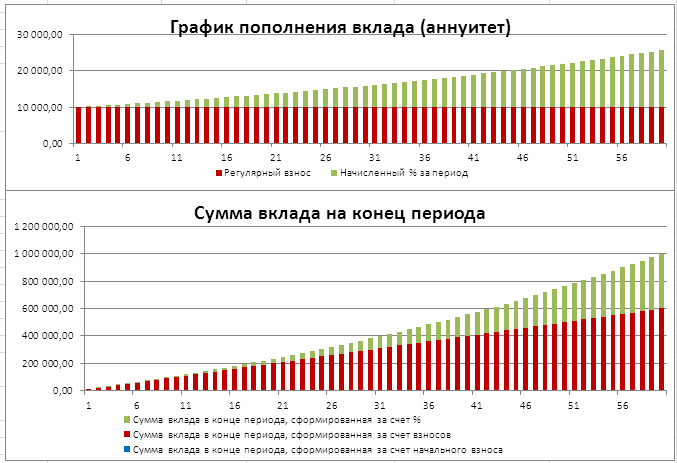
Если суммарное количество взносов будет > целевой стоимости (1000000), то ставка станет отрицательной, чтобы соблюсти наше требование БС=1000000.

Если задать величину пополнения = 0 или того же знака, что и целевая сумма, то функция СТАВКА() вернет ошибку #ЧИСЛО! Это и понятно, при нулевых взносах накопить ничего не получится. Взнос того же знака, что и целевая сумма, вероятно, означает, что банк платит нам. Но, это не возможно, т.к. начальная сумма вклада =0, поэтому выдается ошибка.

Расчет в Excel суммы кредита для заданного аннуитетного платежа

В чём «фишка» аннуитетной схемы погашения кредита? Правильно! Основная «фишка» в том, что заёмщик выплачивает кредит равными суммами на протяжении всего срока кредитования. С такой схемой очень удобно планировать свой бюджет. Например, вы готовы ежемесячно выделять на погашение кредита 5000 рублей. По вашим скромным подсчётам, такая нагрузка будет для вас не слишком обременительной. Естественно, у вас возникает закономерный вопрос: «А на какую сумму кредита я могу рассчитывать?» В общем, нам нужен новый кредитный калькулятор, у которого в исходных данных будет не сумма кредита, а величина аннуитетного платежа.

Что же, друзья, не будем терять время! Открываем программу Microsoft Excel и приступаем к разработке нашего кредитного калькулятора!

Итак, структура нового кредитного калькулятора почти не изменилась. Здесь также есть блок с исходными данными и блок с расчётами. Единственное изменение, это то, что в исходных данных мы вводим ежемесячный аннуитетный платёж, который готовы выплачивать, а в расчётах получаем сумму кредита, на которую мы можем рассчитывать. Собственно, она на нашем рисунке обведена и отмечена под номером 1.

Чтобы рассчитать сумму ожидаемого кредита надо воспользоваться функцией ПС, предварительно кликнув по ячейке, в которой мы хотим видеть свой расчёт (в нашем калькуляторе это ячейка с координатой C11). Вызвать функцию ПС можно нажав на знакомую вам кнопку «fx», которая находится слева от строки формул. В появившемся окне выбираем «ПС» и жмём «Ок». В открывшейся таблице вводим следующие данные:

• «Ставка» – годовая процентная ставка по кредиту делённая на 12 (в нашем случае: C5/12).
• «Кпер» – общий срок кредитования (в нашем калькуляторе, это ячейка с координатой C6).
• «Плт» – ежемесячный аннуитетный платёж, перед которым ставим знак минус (в нашем калькуляторе, это ячейка C4, перед данной координатой мы и ставим знак минус).

Жмём «Ок» и в ячейке С11 появилась сумма 53 422 руб. – именно на такой размер кредита может рассчитывать заёмщик, который готов на протяжении 12 месяцев ежемесячно выплачивать по 5000 руб.

Кстати, обратите внимание на данные в строке формул (на рисунке они обведены и указаны под номером 2). Вы всё правильно поняли, друзья! Да, это те данные, которые необходимы для расчёта суммы кредита в нашем калькуляторе: =ПС(C5/12;C6;-C4). Те самые параметры, которые мы вводили в таблице функции ПС

Те самые параметры, которые мы вводили в таблице функции ПС.

Расчёт остальных показателей выполняется по такому же принципу, как и в предыдущем калькуляторе:

• Общая сумма выплат – это ежемесячный аннуитетный платёж (ячейка С4) умноженный на общий срок кредитования (ячейка С6). В строку формул вводим следующие данные: =C4*C6.
• Переплата (проценты) по кредиту – это общая сумма выплат (ячейка С12) минус сумма кредита (ячейка С11). В строку формул записываем: =C12-C11.
• Эффективная процентная ставка (или полная стоимость кредита) – это общая сумма выплат (ячейка С12) делённая на сумму кредита (ячейка С11) и минус единица. Затем всё это делим на срок кредитования, выраженный в годах (ячейка C6 делённая на 12). В строку формул записываем: = (C12/C11-1)/(C6/12).

Кстати, интересный момент. Вот в нашем примере, выплачивая ежемесячно в течение года по 5000 рублей, мы можем рассчитывать на сумму кредита равную 53 422 рубля. А что делать, если надо больше денег? Как вариант, можно увеличить срок кредитования. Если вместо 12 месяцев поставить 24, то сумма кредита увеличится до 96 380 рублей. Эти данные нам мгновенно выдал наш кредитный калькулятор, который вы можете скачать ссылке ниже:

Скачать калькулятор расчёта суммы аннуитетного кредита в Excel

Подбор параметра для банковских кредитов

Допустим, Вы хотите приобрести автомобиль в кредит. Максимальная сумма ежемесячного взноса, которую Вы можете себе позволить, составляет 700$. Банк не может выдать Вам кредит сроком более чем на 3 года, с процентной ставкой 5,5% годовых. Можете ли вы себе позволить при таких условиях кредитования приобрести автомобиль стоимостью в 30 000$, а если нет, то на какую сумму можно рассчитывать?

Составьте таблицу условий кредитования в Excel как показано ниже на рисунке

Обратите внимание! Ячейка B4 содержит формулу: =-ПЛТ(B3/12;B2;B1)

Как видно Вы не можете себе позволить такой дорогой автомобиль. Теперь узнаем, какая максимальная стоимость автомобиля соответствует Вашим финансовым возможностям. Для этого перейдите в ячейку B4 и выберите инструмент: «Данные»-«Работа с данными»-«Анализ что если»-«Подбор параметра».

Заполните поля в появившемся диалоговом окне как показано выше на рисунке и нажмите ОК.

Как видно максимальная стоимость автомобиля, на которую можно рассчитывать составляет при таких финансовых возможностях и условиях кредитования составляет – 23 1812$.

Внимание! Если срок кредитования определяется количеством месяцев, а не лет, то годовую процентную ставку нужно перевести в месячную. Поэтому в первом аргументе функции ПЛТ стоит значение B3/12 (5,5% годовых разделено на 12 месяцев)

Используя финансовые функции, следует помнить об их стандартах. Например, сумма займа всегда отображаются как отрицательное число. Поэтому перед функцией ПЛТ мы использовали знак минус.

Кредитный калькулятор в Excel

Каждая финансовая компания, имеющая собственный сайт, предлагает пользователям опцию расчетов по кредитам. Воспользовавшись сервисом, потенциальный заемщик сможет наглядно увидеть размер своего текущего платежа, а так же общую сумму, которую он должен будет вернуть банку. Конечно, пользоваться таким программами легко и довольно удобно, однако желательно все же иметь собственного, домашнего помощника в подсчетах. Идеальный вариант – специальная программа, разработанная в Excel.

Данный сервис – это калькулятор, который даст возможность быстро посчитать различные виды выплат по кредитному соглашению, не требуя при этом прямого доступа к интернет-ресурсу. Человеку просто необходимо скачать приложение и выполнять математические подсчеты в любое удобное для него, время.

Обратите внимание! Программа достаточно популярна в бухгалтерском учете. Для того чтобы получить данные, потребуется минимум информации:

Для того чтобы получить данные, потребуется минимум информации:

• величина планируемого займа;
• целевое предназначение сделки;
• процентная ставка, действующая в банке на данный момент времени.

Программа выглядит в виде таблицы, поля которой заполняются данными. При работе с ней используются следующие функции:

• КПЕР – размер кредита в рублях;
• СТАВКА – величина переплаты. Измеряется в процентах на определенный промежуток времени. Чаще всего – за год;
• ПС – целевое предназначение займа;
• ПЛТ – текущий взнос по кредиту.

Если ввести в программу верхние три пункта, сервис в автоматическом режиме подсчитает последний, четвертый.

Справка! В программе так же есть опция составления персонального графика внесения денег на счет банка. Для этого дополнительно потребуется дата, с которой начал свое действие договор по займу. Она указывается в соглашении, подписанном сторонами.

Правила использования функции ОСПЛТ в Excel

Функция ОСПЛТ имеет следующий синтаксис:

=ОСПЛТ(ставка;период;кпер;пс;;)

Описание аргументов:

• ставка – обязательный для заполнения, принимает числовое значение процентной ставки в отношении финансового продукта (например, банковского кредита. Задается в виде десятичной дроби. Например, если кредит был взят по 17%, необходимо ввести значение 0,17;
• период – обязательный для заполнения, принимает числовые значения из диапазона от 1 до числа, указанного в качестве следующего аргумента рассматриваемой функции (кпер);
• кпер – обязательный для заполнения, принимает числовое значение, указывающее число периодов платежей в отношении финансового продукта;
• пс – обязательный для заполнения, принимает значение текущей стоимости финансового продукта, то есть суммы кредита, которую клиент должен вернуть банковской организации после заключения договора;
• – необязательный для заполнения, принимает значение будущей стоимости финансового продукта на момент совершения последнего платежа по утвержденной схеме платежей. Если явно не указан, принимается значение, равное 0 (нулю). Значение 0 означает, что задолженность будет выплачена в полном объеме;
• – необязательный для заполнения, принимает значения 0 или 1, указывающие на способ совершения платежей (в конце или начале периода). Если явно не указан, принимает значение 0.

Примечания:

1. Если аргумент период принимает значение не из диапазона , функция ОСПЛТ вернет код ошибки #ЧИСЛО!
2. Обязательные аргументы могут быть указаны в виде чисел, а также значений текстовых или других типов данных, которые могут быть преобразованы к числовым. Например, записи =ОСПЛТ(0,12;ИСТИНА;12;1000) или =ОСПЛТ(0,17;«4»;10;32000) являются допустимыми.
3. При указании аргументов ставка и кпер необходимо согласовывать единицы измерения этих показателей с учетом периодичности выплат. Например, для кредита, оформленного сроком на 1 год со ставкой 23% и ежемесячными платежами аргументы ставка и кпер функции ОСПЛТ должны быть заданы как 0,23/12 и 1*12 соответственно.

Заключение

Рассчитать ипотечный кредит в состоянии каждый потенциальный заявитель. Для этого ему предлагается калькулятор в excel, который поможет справиться с ежемесячными погашениями. Универсальное средство учитывает не только тело кредита, но и ставку процента.

Используйте наш ипотечный калькулятор с досрочным гашением, чтобы сравнить ваши результаты, а также прочитайте информацию о том, стоит ли брать ипотеку в 2018 году.

Запись на бесплатную консультацию в специальной форме в углу.

Просьба оценить пост и нажать кнопки соцсетей.

Did you find apk for android? You can find new Free Android Games and apps.