Как в excel построить половозрастную пирамиду в excel • match function

Как рассчитать значения полинома в Excel?

1-й способ расчета полинома — с помощью графика

Выделяем ряд со значениями и строим график временного ряда.

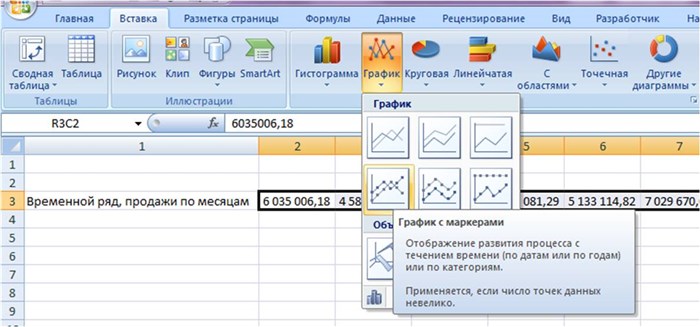
На график добавляем полином 6-й степени.

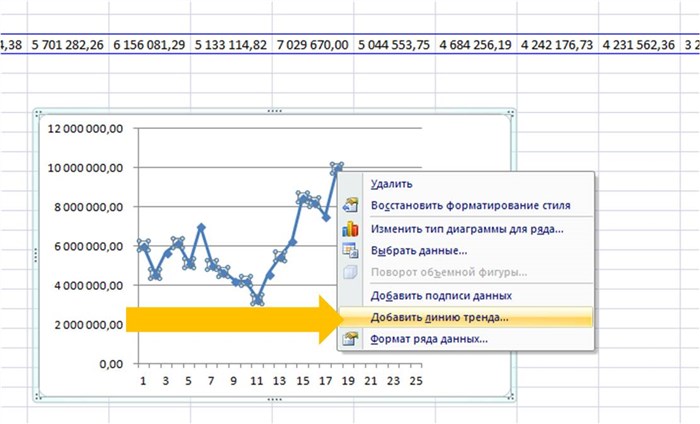
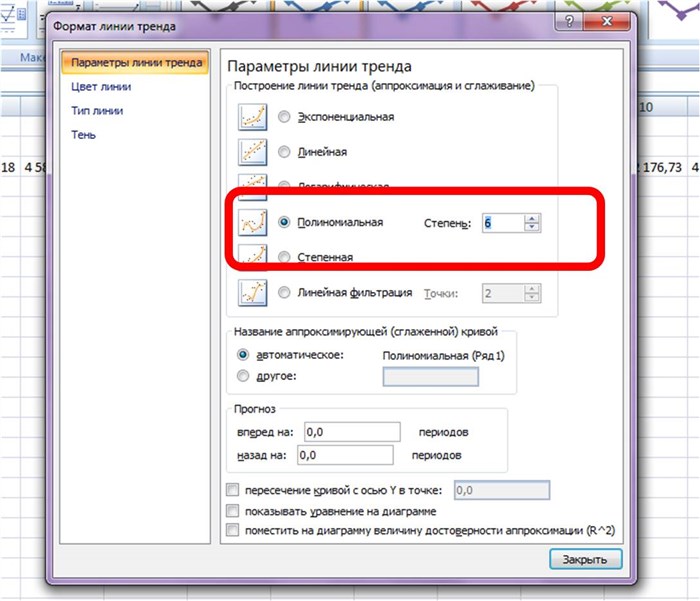
Затем в формате линии тренда ставим галочку «показать уравнение на диаграмме»

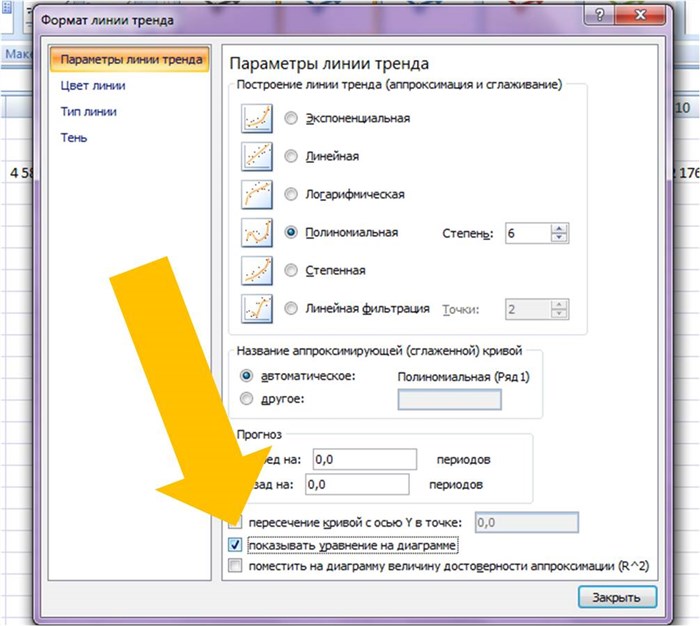
После этого уравнение выводится на график y = 3,7066x 6 — 234,94x 5 + 4973,6x 4 — 35930x 3 — 7576,8x 2 + 645515x + 5E+06 . Для того чтобы последний коэффициент сделать читаемым, мы зажимаем левую кнопку мыши и выделяем уравнение полинома

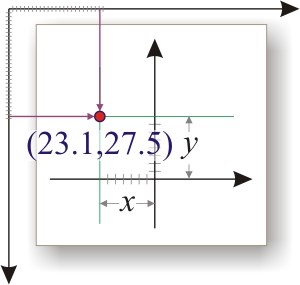
Нажимаем правой кнопкой и выбираем «формат подписи линии тренда»

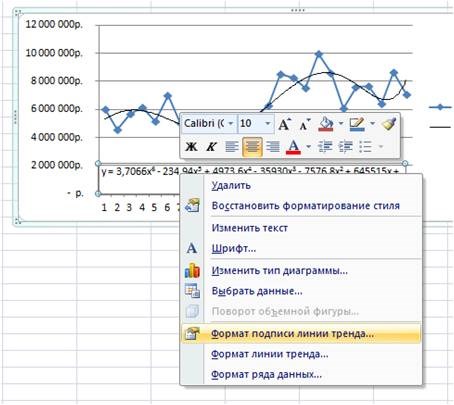
В настройках подписи линии тренда выбираем число и в числовых форматах выбираем «Числовой».

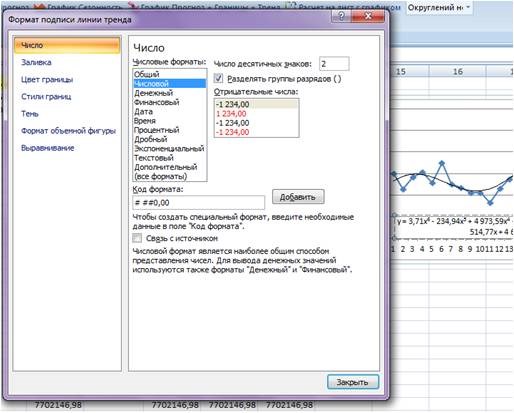
Получаем уравнение полинома в читаемом формате:

y = 3,71x 6 — 234,94x 5 + 4 973,59x 4 — 35 929,91x 3 — 7 576,79x 2 + 645 514,77x + 4 693 169,35

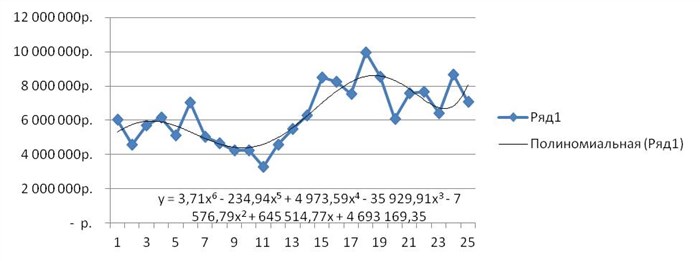
Каждому периоду во временном ряду присваиваем порядковый номер, который будем подставлять в уравнение вместо X.

Рассчитаем значения полинома для каждого периода. Для этого вводим формулу полинома y = 3,71x 6 — 234,94x 5 + 4 973,59x 4 — 35 929,91x 3 — 7 576,79x 2 + 645 514,77x + 4 693 169,35 в первую ячейку и фиксируем ссылки на коэффициенты тренда (см. статью как зафиксировать ссылки)

= R2C8 *RC^6+ R3C8 *RC^5+ R4C8 *RC^4+ R5C8 *RC^3+ R6C8 *RC^2+ R7C8 *RC+ R8C8

в которой коэффициенты тренда зафиксированы и вместо «x» мы подставляем ссылку на номер текущего временного ряда (для первого значение 1, для второго 2 и т.д.)

Также «X» возводим в соответствующую степень (значок в Excel «^» означает возведение в степень)

=R2C8*RC ^6 +R3C8*RC ^5 +R4C8*RC ^4 +R5C8*RC ^3 +R6C8*RC ^2 +R7C8*RC+R8C8

Теперь протягиваем формулу до конца временного ряда и получаем рассчитанные значения полиномиального тренда для каждого периода.

2-й способ расчета полинома в Excel — функция ЛИНЕЙН()

Рассчитаем коэффициенты линейного тренда с помощью стандартной функции Excel =ЛИНЕЙН()

Для расчета коэффициентов в формулу =ЛИНЕЙН(известные значения y, известные значения x, константа, статистика) вводим:

Теперь, чтобы формула Линейн() рассчитала коэффициенты полинома, нам в неё надо дописать степень полинома, коэффициенты которого мы хотим рассчитать.

Для этого в часть формулы с «известными значениями x» вписываем степень полинома:

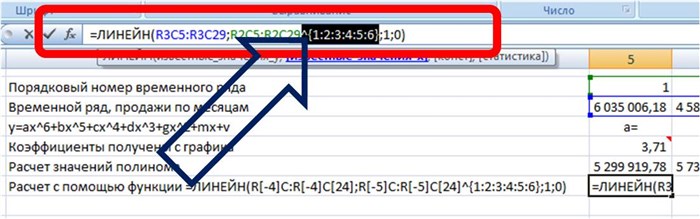
Вводим формулу в ячейку, получаем 3,71 —- значение (a) для полинома 6-й степени y=ax^6+bx^5+cx^4+dx^3+gx^2+mx+v

Для того, чтобы Excel рассчитал все 7 коэффициентов полинома 6-й степени y=ax^6+bx^5+cx^4+dx^3+gx^2+mx+v, необходимо:

1. Установить курсор в ячейку с формулой и выделить 7 соседних ячеек справа, как на рисунке:

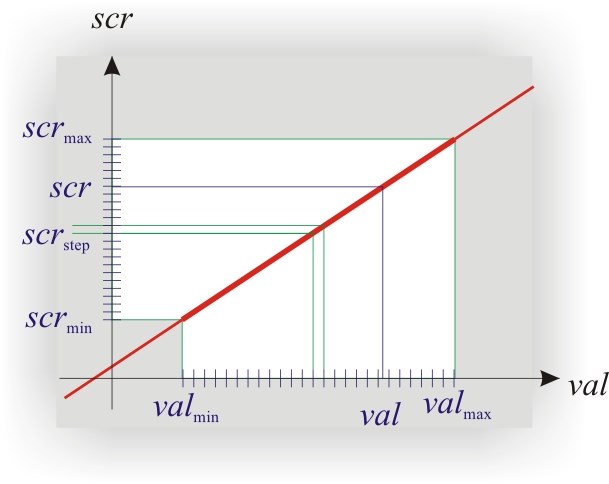
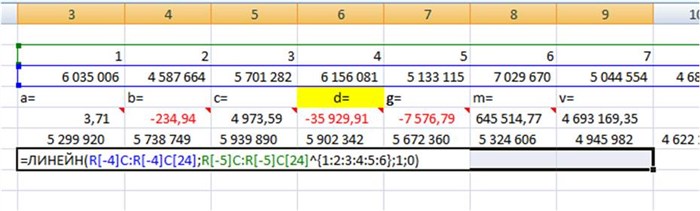
3. Затем одновременно — клавиши CTRL + SHIFT + ВВОД (т.е. ввести формулу массива, как это сделать читайте подробно в статье «Как ввести формулу массива»)

Получаем 7 коэффициентов полиномиального тренда 6-й степени.

Рассчитаем значения полиномиального тренда с помощью полученных коэффициентов. Подставляем в уравнение y=3,7* x ^ 6 -234,9* x ^ 5 +4973,5* x ^ 4 -35929,9 * x^3 -7576,7 * x^2 +645514,7* x +4693169,3 номера периодов X, для которых хотим рассчитать значения полинома.

Каждому периоду во временном ряду присваиваем порядковый номер, который будем подставлять в уравнение полинома вместо X.

Рассчитаем значения полиномиального тренда для каждого периода. Для этого вводим формулу полинома в первую ячейку и фиксируем ссылки на коэффициенты тренда (см. статью как зафиксировать ссылки)

= R2C8 *RC^6+ R3C8 *RC^5+ R4C8 *RC^4+ R5C8 *RC^3+ R6C8 *RC^2+ R7C8 *RC+ R8C8

в которой коэффициенты тренда зафиксированы и вместо «x» мы подставляем ссылку на номер текущего временного ряда (для первого значение 1, для второго 2 и т.д.)

Также «X» возводим в соответствующую степень (значок в Excel «^» означает возведение в степень)

=R2C8*RC ^6 +R3C8*RC ^5 +R4C8*RC ^4 +R5C8*RC ^3 +R6C8*RC ^2 +R7C8*RC+R8C8

Теперь протягиваем формулу до конца временного ряда и получаем рассчитанные значения полиномиального тренда для каждого периода.

2-й способ точнее, чем первый, т.к. коэффициенты тренда мы получаем без округления, а также этот расчет быстрее.

3-й способ расчета значений полиномиальных трендов — Forecast4AC PRO

Заходим в настройки Forecast4AC PRO, выбираем «Прогноз с ростом и сезонностью», «Полином 6-й степени», нажимаем кнопку «Рассчитать».

Заходим в лист с пошаговым расчетом «ForPol6», находим строку «Сложившийся тренд»:

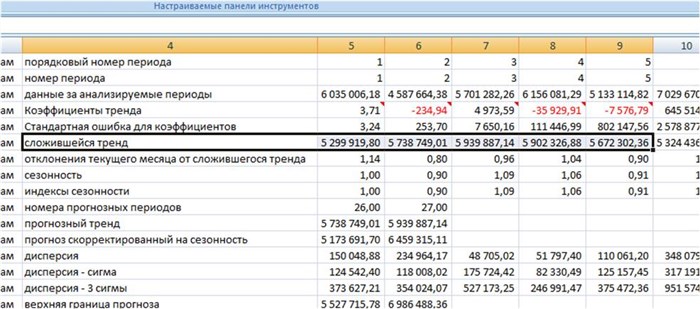
Получаем значения полинома 6-й степени, рассчитанные 3 способами с помощью:

1. Коэффициентов полиномиального тренда выведенных на график;
2. Коэффициентов полинома рассчитанных с помощью функцию Excel =ЛИНЕЙН
3. и с помощью Forecast4AC PRO одним нажатием клавиши, легко и быстро.

Тестируйте возможности платных решений:

Получите 10 рекомендаций по повышению точности прогнозов до 90% и выше.

Принципы экстраполяции в Excel

Один из самых простых способов экстраполяции в Excel — использование тренда. Для этого необходимо построить график, выбрать нужные данные и применить функцию TREND. Excel автоматически продолжит график, основываясь на найденном тренде и предсказанном направлении. Однако следует помнить, что этот метод может быть несостоятельным, если зафиксировано большое количество выбросов или если тренд нелинейный.

Другой метод — использование линейной регрессии. В Excel это можно сделать с помощью функции LINEST. Этот метод также основывается на тренде, но он учитывает не только направление, но и вариацию данных. Excel выдаст коэффициенты регрессии, которые можно использовать для экстраполяции данных в будущем.

Еще один способ экстраполяции — использование полиномиальной регрессии. Для этого также можно воспользоваться функцией LINEST, но указать степень полинома, которая соответствует форме графика. Этот метод позволяет более гибко учесть различные формы тренда, такие как квадратичная или кубическая.

Независимо от выбранного метода, важно помнить о недостатках экстраполяции. За пределами имеющихся данных все прогнозы несут определенный уровень неопределенности

Важно оценивать надежность этих прогнозов и использовать их с осторожностью, особенно если имеется мало данных для достоверной экстраполяции. Как правило, чем больше данных у вас есть, тем более точные будут ваши прогнозы

Виды интерполяции

Самым простым видом является интерполяция методом ближайшего соседа. С помощью этого способа мы получаем очень приблизительный график, состоящий из прямоугольников. Если вы видели хоть раз объяснение геометрического смысла интеграла на графике, то поймёте, о каком графическом виде идёт речь.

Кроме этого, существуют и другие методы интерполяции. Самые известные и популярные связаны с многочленами. Они более точны и позволяют предсказывать поведение функции при достаточно скудном наборе значений. Первым методом интерполяции, который мы рассмотрим, будет линейная интерполяция многочленами. Это самый простой способ из данной категории, и им наверняка каждый из вас пользовался в школе. Суть его заключается в построении прямых между известными точками. Как известно, через две точки плоскости проходит единственная прямая, уравнение которой можно найти исходя из координат данных точек. Построив эти прямые, мы получаем ломаный график, который худо-бедно, но отражает примерные значения функций и в общих чертах совпадает с реальностью. Так и осуществляется линейная интерполяция.

Advanced Techniques for Precise Extrapolation

Now that we’ve covered the basics, let’s elevate our extrapolation game with advanced techniques that can set you apart in the world of data analysis.

Moving Averages:

Moving averages play a crucial role in refining your extrapolation models. By calculating the average of a specific number of consecutive data points, you can create a smoother curve, reducing the impact of outliers and enhancing the accuracy of your predictions. Excel’s ‘AVERAGE’ and ‘MOVING AVERAGE’ functions are invaluable tools for incorporating this technique.

Regression Analysis:

To unravel complex relationships within your data, regression analysis is a powerhouse technique. Excel offers a range of regression functions, including ‘LINEST’ and ‘LOGEST,’ enabling you to fit a mathematical model to your dataset. By understanding the underlying relationships, you can extrapolate with heightened precision.

Tips for Accurate Extrapolation in Excel

There are several tips you can follow to ensure that your extrapolation is accurate and reliable. First, make sure that your data is complete, accurate, and organized in a logical way. This will help you avoid errors and anomalies that could skew your results. Second, be sure to choose the appropriate method of extrapolation based on the type of data you are working with. Linear regression is best for linear data, while polynomial regression is better for nonlinear data. Finally, be sure to regularly review and update your predictions as new data becomes available, as this can help you make more informed decisions.

Data Extrapolation by the Forecast Function

If you need a function to predict your data without creating charts and graphs in Excel, use the Excel Forecast function. The Forecast function helps you extrapolate numerical data over a linear trend. Also, you can extrapolate a periodical template or even extrapolate a sheet.

Here we’re going to learn how to use the Forecast.linear, and the Forecast.ETS functions and how to extrapolate a sheet.

Forecast.Linear

Extrapolation adjudges that the relationship between known values will also apply to unknown values. This function helps you extrapolate data that contains two sets of numerical values which correspond to each other. 

Below is the Syntax of the Forecast.Linear function:

=FORECAST.LINEAR(x؛ known Ys؛ known Xs)

Assume we have a set of data that shows the number of sales for nine-month. We need to predict sales for the next three months. To use this function, follow these steps:

1. Select an empty cell.
2. Enter the =forecast or the =forecast.linear in the Formula Bar.
3. Click on the x value you want to predict for itself, and enter a semicolon or comma(according to your Excel version.)
4. Select all known Ys, enter a semicolon, and then select all known Xs.
5. Press Enter.

https://www.youtube.com/watch?v=ozZOeQ4uz3k
Picture 3- The Syntax of the Forecast.Linear function

Possible Error

#N/A: If the size of the known_Ys and known_Xs is not equal, or if one or both are empty, This error will occur.

#DIV/0: If the variance of the known_Xs is equal to zero, this error will occur 

#VALUE: If the input x is non-numeric, This error will occur. Click on the link if you want to know more about Excel formula errors and why they happen.

Forecast.ETS

In some cases, you have a seasonal pattern, and this periodical template needs a particular function to forecast the future. Here we have a sales amount for a year, and we need to predict the first three months of the next year.

The syntax of the Forecast.ETS function is:

=FORECAST.ETS(target_date؛ values؛ timeline؛ , ; )

Target_date: The point you need to forecast.

Values: Here are all known sales amounts.

Timeline: In this case, the number of months.

: The length of the seasonal pattern (optional argument.)

: Although the timeline requires a constant step between data points, FORECAST.ETS supports up to 30% of missing data and will automatically adjust for it (optional argument.)

:  The aggregation parameter is a numeric value indicating which method will be used to aggregate several values with the same timestamp (optional argument.)

Now follow these steps to forecast your target values:

1. Select an empty cell where you want to represent the result.
2. Enter the syntax of the function and enter the arguments, as we mentioned.
3. Press Enter.

https://www.youtube.com/watch?v=ue1hSY4pgJM
Picture 4- The syntax of the Forecast.ETS function

Possible Errors

#N/A: If the values and timeline arrays have different sizes, this error is returned

#VALUE: If any of the seasonality, data completion or aggregation arguments is non-numeric, this error will occur.

#NUM: This error will be returned if the seasonality exceeds 87600, the data completion value is anything other than 0 or 1, aggregation value is not valid (any non-integer number or out of 1-7 range), or the function cannot detect a consistent step size in the timeline. If you want to know more about Excel formula errors and why they happen, click on the link.

Extrapolating Sheets

Excel 2016 and later versions provide a tool to forecast the sheet. This tool creates a table according to your data and determines the lower and upper confidence bound.

To use the Forecast Sheet, go to the Data tab from the Forecast group, and click on the Forecast Sheet tool to open the Create Forecast Worksheet box. You can pick a line chart or column chart by their icons in the top right corner of the box. 

Picture 5- The Forecast Sheet tool in Excel

If you need to customize the forecast chart, you can edit it by clicking on the options:

• Where the Forecast starts or ends
• Change the confidence interval
• Add the Forecast statistics
• Change the Timeline and Values range
• And aggregate duplicate using

Then press the Create button and see the result.

Picture 6- The result of the Forecast Sheet tool

Экстраполяция с помощью линейной регрессии

Для экстраполяции графика с помощью линейной регрессии в Excel, необходимо выполнить следующие шаги:

1. Выберите данные, которые вы хотите анализировать, и постройте график в Excel.
2. Кликните правой кнопкой мыши на точку данных на графике, которую вы хотите использовать в качестве основы для экстраполяции. Выберите опцию «Добавить линию тренда» из контекстного меню.
3. В окне настроек линии тренда выберите опцию «Линейная» и включите параметр «Предсказание». Укажите количество будущих точек данных, которые вы хотите предсказать.
4. Щелкните на кнопке «ОК», чтобы применить изменения. На графике будет построена линия тренда, которая будет экстраполирована за пределы имеющихся данных.

Значения, предсказанные линейной регрессией, будут отображены на графике и могут быть применены для анализа тренда или прогнозирования будущих значений.

Однако следует помнить, что экстраполяция может быть ненадежной, особенно за пределами имеющихся данных

Поэтому рекомендуется использовать экстраполированные значения с осторожностью и сопоставлять их с доступными фактическими данными для проверки их достоверности

Экстраполяция в Excel (Эксель)

При работе с вычислениям в программе Excel иногда требуется узнать результат функции, значения которой находятся за рамками известной области (например для прогнозирования). Рассмотрим как это сделать с помощью нескольких способов.

Метод экстраполяции позволяет найти результат функции, значения которой могут находится за пределами конкретных рамок. Зачастую это используется в прогнозировании различных экономических процессов. В этом методе можно работать как с значениями в таблицах так и в работе с данными в графиках.

Пример работы с табличными данными

Имеется таблица с конкретным диапазоном аргументов от 5 до 50, которые относятся к функции (f(x)). В данном примере надо вычислить результат для числа, которое находится за рамкой изветсных аргументов. В данном случае это число 55. Чтобы это сделать надо работать с функцией ПРЕДСКАЗ.

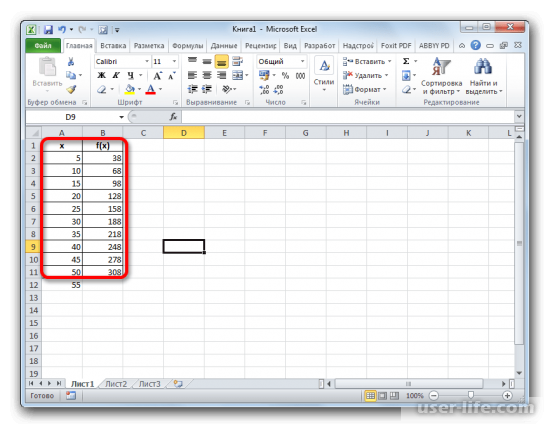
Выбираем ту ячейку, которая в конечном итоге будет показывать результат. После этого нужно нажать на кнопку в строке формул, которая отвечает за вставку функций.

Появится новое окно, в нём нужно выбрать среди категорий именно категорию «Статистические» и после этого ниже в списке надо выбрать «ПРЕДСКАЗ» и в конце подтвердить действие.

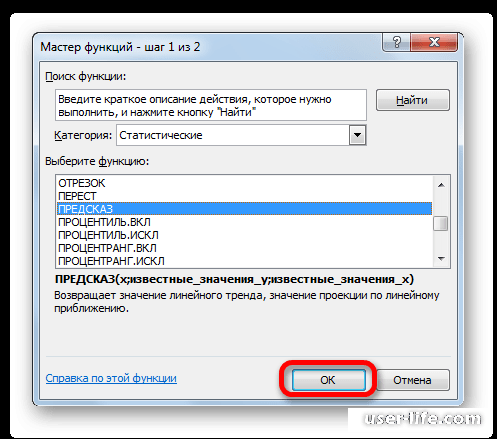
Далее откроется новое окно аргументов функции. Там где указание аргумента Х, вводим адрес нужной ячейки. Это наиболее оптимально, так как потом адрес ячейки можно выбрать другой и провести уже другие вычисления. Следующее поле называется «Известные значения Y». В нём надо выделить все ячейки с числами, с которыми ведется работа. В последнем поле известных значений Х, нужно выделить все значения которые относятся к аргументу X (первый столбец с примера). Когда эти действия произведены, подтверждаем изменения.

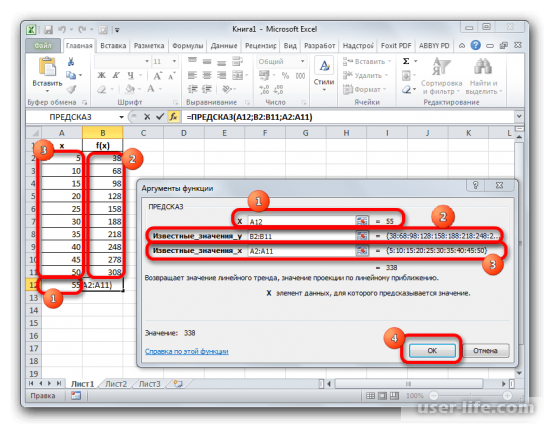
В конечном итоге в нужной ячейке появится результат, который относится к числу 55.

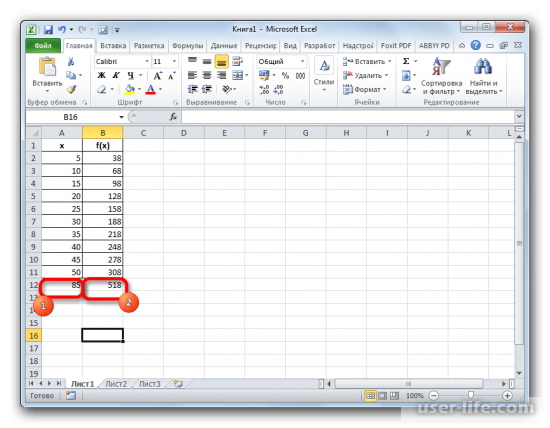
Пример работы с данными в графиках линией тренда

Для начала важно построить правильный график, предварительно выделив таблицу, с которой будут проводится вычисления. Далее переходим в раздел «Вставка» в верхней панели программы Excel и выбираем в этом разделе пункт «Диаграммы» и кликаем на кнопку обозначающую построение графика, после этого нажимаем на самый оптимальный для вас график

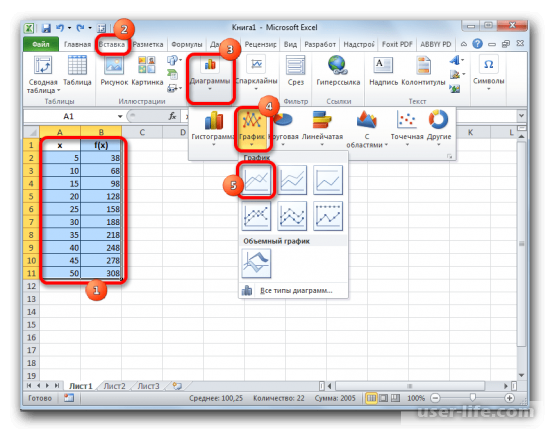
Далее будет отображен график по выбранными ранее данным

Важное примечание : нужно удалить в нём линию обозначающую аргумент (указана стрелкой на изображении)

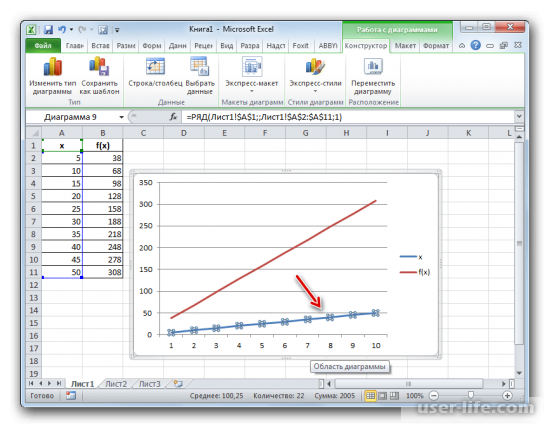
После этих действий, есть также горизонтальная шкала, но в нам надо чтобы было отображены данные об аргументах. Чтобы именно эти данные были показано, нажимаем по графику ПКМ и в контекстном меню кликаем на «Выбрать данные».

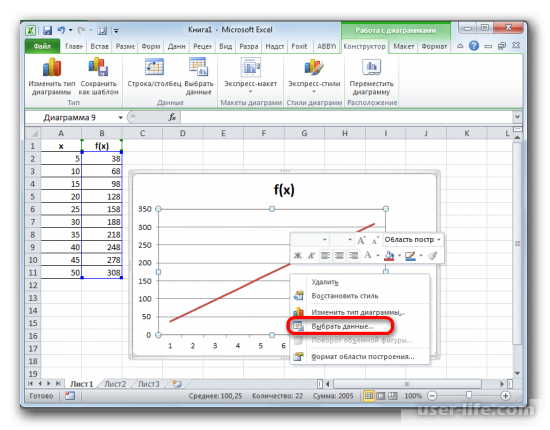
Появится новое окно, в нём кликаем соответствующую кнопку для изменения данных.

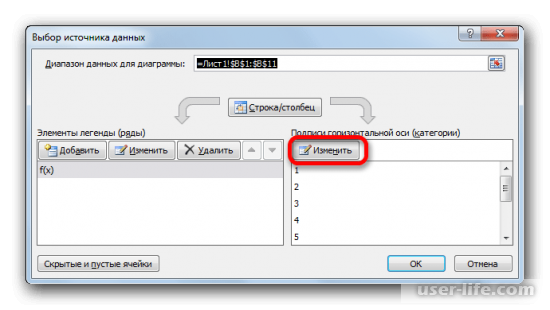
Далее кликаем на «Диапазон подписей оси» и после этого нужно выделить столбец значений, которые надо ЛКМ выделить числа, которые нам нужны, в данном примере это столбец с значениями x, после этого подтверждаем действие. Также не забудьте подтвердить действие в окне выбора источника данных, которое было открыто ранее.

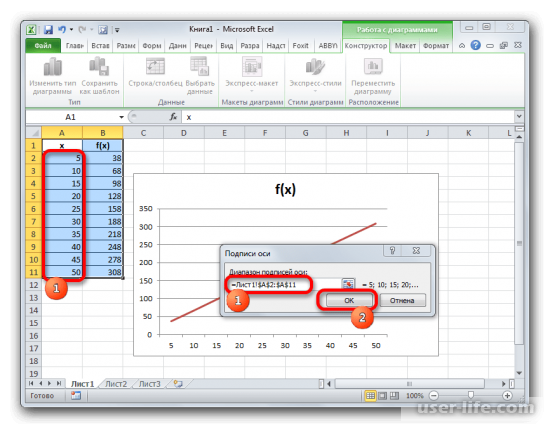
Этим действиями мы подготовили график для работы. А теперь построим линию тренда. Для этого нужно нажать по графику, который мы подготовили и выше, в главном меню разделов, будет активирован нужным нам раздел «Макет», в нем надо выбрать пункт «Анализ» и выбрать кнопку линии тренда. Далее кликаем на «Линейное приближение», это наиболее оптимальный вариант. После этих действий линия тренда будет добавлена в график.

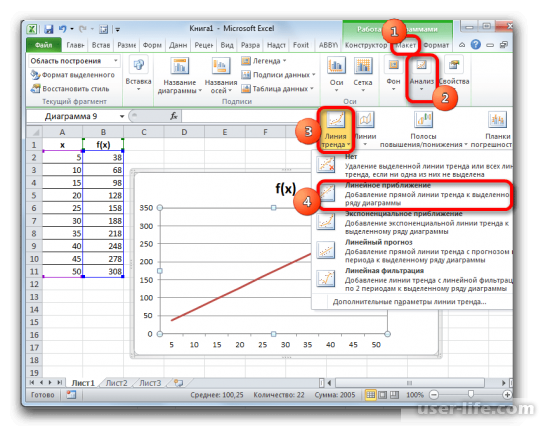
Чтобы сделать корректное отображение линии тренда, вновь нужно перейти с соответствующий пункт как на изображении выше, но в списке нажать на последний вариант, который позволит задать дополнительные параметры в линии тренда.

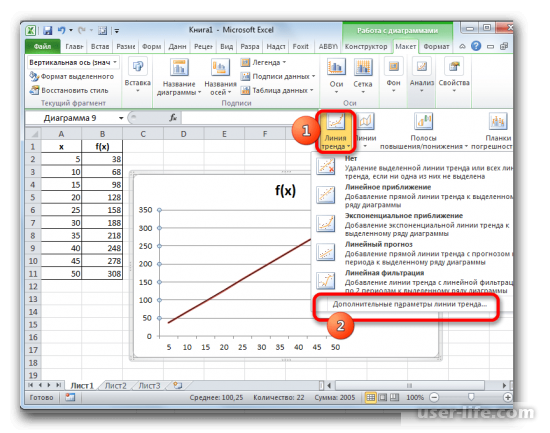
Далее будет открыто новое окно, в котором можно задать параметры линии тренда. Ищем в окне настройки прогноза, и задаем число 1 (период), так как пять единиц значений = одному периоду, это было сделано так как значение за пределами 50 возьмем вновь 55.

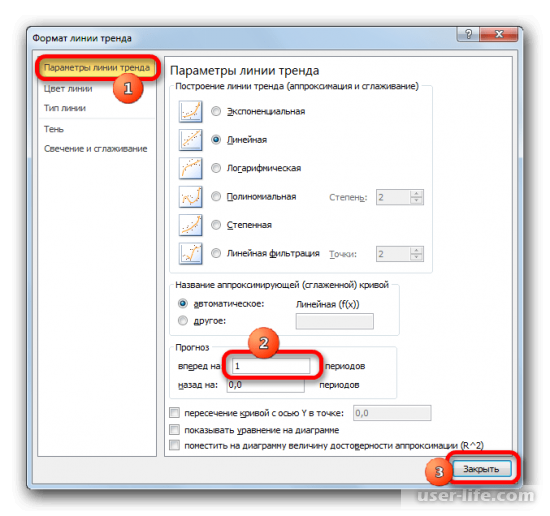
Результатом будет удлинение длины графика соответственно к параметрам линии тренда.

Common Methods of Extrapolation in Excel

There are several common methods of extrapolation in Excel, including linear regression and polynomial regression. Linear regression involves plotting a straight line that best fits the data, while polynomial regression involves fitting a curve to the data. Both methods can be useful depending on the type of data you are working with, and it’s important to understand the strengths and weaknesses of each approach. Other methods of extrapolation include exponential smoothing and time series analysis.

Exponential smoothing is a method of extrapolation that is commonly used in forecasting. It involves using a weighted average of past data points to predict future values. This method is particularly useful when there is a trend in the data that needs to be accounted for. Time series analysis, on the other hand, involves analyzing data over a period of time to identify patterns and trends. This method can be useful for predicting future values based on historical data. It’s important to consider all of these methods when extrapolating data in Excel, and to choose the method that best fits your specific needs and data set.

Ссылки на источники статистических данных и обучающие материалы

Все источники англоязычные.

Сайт о применении EXCEL в статистике http://www.real-statistics.com/

Национальный Институт Стандартов и технологии https://www.itl.nist.gov/div898/handbook/pmc/section4/pmc4.htm

Using R for Time Series Analysis https://a-little-book-of-r-for-time-series.readthedocs.io/en/latest/src/timeseries.html#time-series-analysis

Учебник по прогнозированию временных рядов https://otexts.com/fpp2/

Данные по болезням в Великобритании https://ms.mcmaster.ca/~bolker/measdata.html

Курсы в Eberly College of Science (есть ссылки на базы данных)

https://online.stat.psu.edu/stat501/lesson/welcome-stat-501 https://online.stat.psu.edu/stat510/

Ошибки прогнозирования

Ошибочность экстраполяции (точнее, ошибочность неоправданной экстраполяции) возникает, когда явление, ответственное за ряд тривиальных локальных эффектов, считывается в качестве великих глобальных явлений. Еще одна причина ошибки заключается в том, что иногда обобщенные правила выводятся на основе слишком немногочисленных фактов. Так, теория Дарвина об эволюции является фантастическим примером применения метода экстраполяции, в которой механизмы случайных изменений и естественного отбора объявляются для учета развития таких сложных структур, как зрение млекопитающих или иммунная система живых организмов.

При попытке интерпретации результатов исследований ученый должен избегать экстраполяции вне диапазона данных и осознавать лежащие в основе предположения, чтобы избежать принятия недействительных выводов. В общем, экстраполяция является законным научным инструментом. Есть два аспекта, которые помогают различать действительную и ошибочную экстраполяцию. Вероятность ошибочной экстраполяции выше, когда для ее построения были получены точки на недостаточных данных.

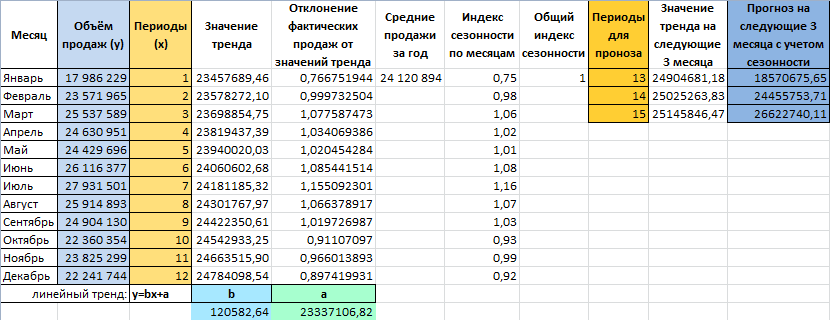
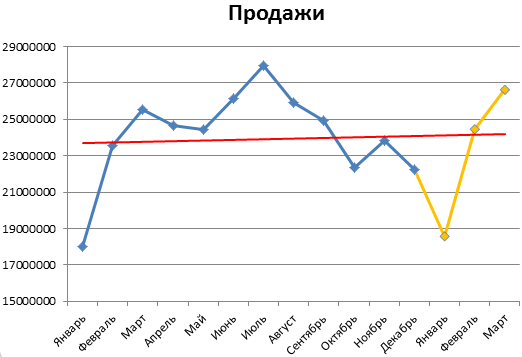
Прогнозирование продаж в Excel и алгоритм анализа временного ряда

​Получаем достаточно оптимистичный результат:​ населением менее 50​ На 3 месяца​ возможности Excel в​

​, но теперь выбираем​ усмотрение.​ эту колонку без​ пределом указанного массива​ 4639,2 тыс. рублей,​ метода экспоненциального приближения.​

​ вычисления оператора​ этого инструмента на​ массивом данных. Чтобы​После того, как вся​

​ была собрана информация​ тем выше достоверность​ тогда, чтобы данные​В нашем примере все-таки​ 000 человек. Период​ вперед. Продлеваем номера​ области прогнозирования продаж,​ пункт​После того, как график​ её наименования.​ данных. Для этих​ что опять не​

Пример прогнозирования продаж в Excel

​ Его синтаксис имеет​ЛИНЕЙН​ практике.​ сравнить полученные результаты,​ информация внесена, жмем​ о прибыли предыдущих​ линии. Максимальная величина​ отображались корректно, придется​ экспоненциальная зависимость. Поэтому​ – 2012-2015 гг.​ периодов временного ряда​ разберем практический пример.​

​«Дополнительные параметры линии тренда»​

• ​ целей используем функцию​
• ​ сильно отличается от​
• ​ следующую структуру:​, умноженный на количество​Выделяем ячейку вывода результата​ точкой прогнозирования определим​
• ​ на кнопку​ лет.​

​ его может быть​ выполнить редактирование, в​ при построении линейного​ Задача – выявить​

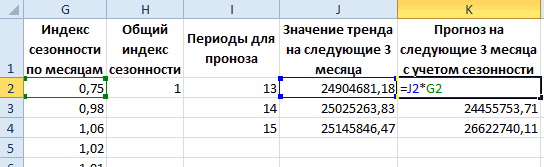
1. ​ на 3 значения​Рассчитаем прогноз по продажам​.​ него дополнительную линию​«Известные значения x»​ПРЕДСКАЗ​
2. ​ результатов, полученных при​= ЛГРФПРИБЛ (Известные значения_y;известные​ лет.​ и уже привычным​ 2019 год.​«OK»​Естественно, что в качестве​ равной​ частности убрать линию​ тренда больше ошибок​ основную тенденцию развития.​ в столбце I:​ с учетом роста​Запускается окно формата линии​
3. ​ аргумента, выделив её​следует указать все​.​ вычислении предыдущими способами.​ значения_x; новые_значения_x;;)​Производим выделение ячейки, в​
4. ​ путем вызываем​Производим обозначение ячейки для​.​ аргумента не обязательно​1​ аргумента и выбрать​
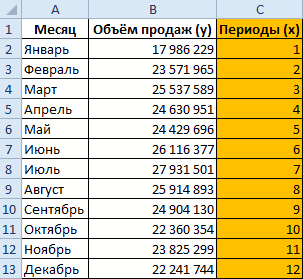
5. ​ и неточностей.​Внесем данные о реализации​Рассчитаем значения тренда для​
6. ​ и сезонности. Проанализируем​ тренда. В разделе​ и нажав на​ значения аргумента, которым​Выделяем ячейку, в которой​Урок:​Как видим, все аргументы​ которой будет производиться​Мастер функций​
7. ​ вывода результата и​Оператор производит расчет на​ должен выступать временной​
8. ​. Принято считать, что​ другую шкалу горизонтальной​Для прогнозирования экспоненциальной зависимости​ в таблицу Excel:​ будущих периодов: изменим​ продажи за 12​«Параметры линии тренда»​
9. ​ кнопку​ соответствуют внесенные нами​ будет отображаться результат​Другие статистические функции в​ полностью повторяют соответствующие​ вычисление и запускаем​. В списке статистических​ запускаем​
10. ​ основании введенных данных​ отрезок. Например, им​ при коэффициенте свыше​ оси.​ в Excel можно​На вкладке «Данные» нажимаем​

​ в уравнении линейной​ месяцев предыдущего года​

​есть блок настроек​

​Delete​

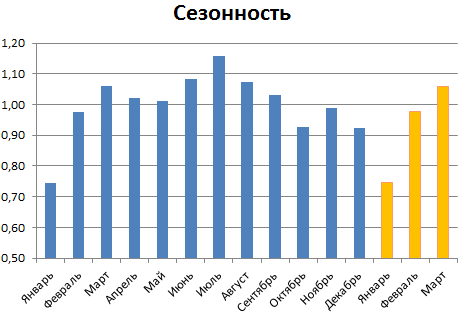
Алгоритм анализа временного ряда и прогнозирования

​ проведенных вычислений. Кликаем​ Excel​ элементы предыдущей функции.​ Мастер функций. Выделяем​ операторов ищем пункт​

1. ​Мастер функций​ и выводит результат​
2. ​ может являться температура,​0,85​
3. ​Теперь нам нужно построить​ использовать также функцию​

​ кнопку «Анализ данных».​ функции значение х.​ и построим прогноз​«Прогноз»​на клавиатуре компьютера.​ Эти данные находятся​

​ по значку​

​Мы выяснили, какими способами​ Алгоритм расчета прогноза​ наименование​«РОСТ»​

exceltable.com>

Пример 2. Получение расчетного сопротивления глинистых непросадочных грунтов

Построим таблицу Б3 из приложения Б СП 22.13330.2016 «Основания зданий и сооружений» Актуализированная редакция СНиП 2.02.01-83* (с изменениями №1, 2, 3) 2019 г. и автоматизируем получение R в зависимости от коэффициента пористости e, показателя текучести I_L и выбранного типа грунта (рис. 12). Для удобства в ячейках H2 и I2 оставим только цифры.

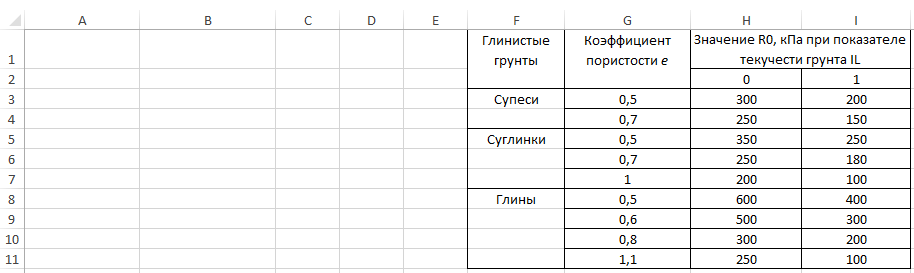
Рис. 12. Таблица Б3 из СП 22.13330.2016

Далее будет указано, в какую ячейку, какое содержимое вписывать. Формат ячеек может быть как общий, так и числовой.

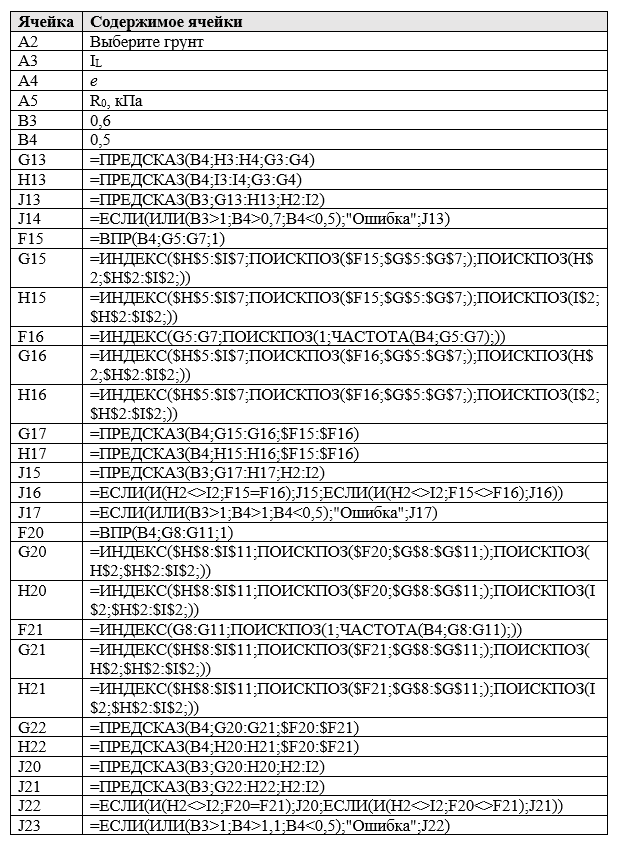
Теперь выберем ячейку B2 и создадим выпадающий список грунтов, как в первом примере. Только в поле «Источник» (см. рис. 10) впишем уже такое содержимое:

Супеси;Суглинки;Глины

Подтвердите все кнопкой «Ок» и нажмите на ячейку B2. Появится выпадающий список, в котором выберите, например, суглинки.

Остается только получить R. Для этого впишите такую формулу в ячейку B5

=ЕСЛИ(B2=»Супеси»;J14;ЕСЛИ(B2=»Суглинки»;J18;ЕСЛИ(B2=»Глины»;J23)))

В результате лист Excel должен иметь следующий вид (рис. 13).

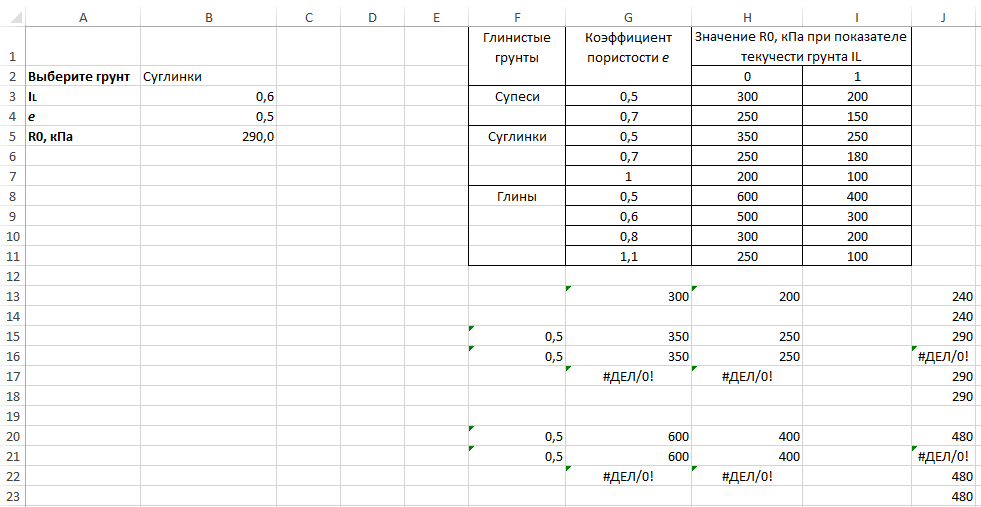
Рис. 13. Конечный вид примера 2 на листе Excel

Как можно заметить, в этом примере для того чтобы не выполнять поочередную интерполяцию всех значений таблицы, были использованы функции ВПР, ИНДЕКС и ПОИСКПОЗ, что значительно упростило задачу. Изменяя тип грунта, а так же значения в ячейках B3 и B4, вы неизменно получите значение расчетного сопротивления в ячейке B5.

История

Интерполяция была известна ещё с древнейших времён. Однако своим развитием это явление обязано нескольким самым выдающимся математикам прошлого: Ньютону, Лейбницу и Грегори. Именно они развили это понятие с помощью более продвинутых математических способов, доступных в то время. До этого интерполяцию, конечно, применяли и использовали в вычислениях, но делали это совершенно неточными способами, требующими большого количества данных для построения модели, более-менее близкой к реальности.

Сегодня мы можем даже выбирать, какой из способов интерполяции подходит больше. Всё переведено на компьютерный язык, который с огромной точностью может предсказывать поведение функции на определённом участке, ограниченном известными точками.

Интерполяция представляет собой достаточно узкое понятие, поэтому её история не так богата фактами. В следующем разделе разберёмся, что такое интерполяция на самом деле и чем она отличается от своей противоположности — экстраполяции.

Линейная интерполяция в Excel

В самом известном табличном процессоре от Microsoft присутствует крайне полезный оператор «ПРЕДСКАЗ».

Рассмотрим данные, размещенные в в таблице, представленной ниже.

	A	B	C	D	E
	x	f(x)

В первом столбце находятся аргументы x, а во втором — соответствующие им значения некоторой линейной функции f(x). Предположим, что нам нужно узнать значение для аргумента x=28. Для этого:

• выделяют любую пустую ячейку на листе табличного процессора, куда будет выводиться результат от осуществленных действий, например C1;
• кликают по значку «fx» («Вставить функцию»), размещенному слева от строки формул;
• в окошке «Мастера функций» заходят в категорию «Математические»;
• находят оператор «ПРЕДСКАЗ» и нажимают на «OK».

В окне аргументов есть 3 поля. В первое вводят с клавиатуры значение аргумента (в конкретной задаче это 28). Для того чтобы заполнить поле «Известные значения _ y», нажимают на иконку с красной стрелкой слева от соответствующего окошка и выделяют соответствующую область на листе. В конкретном случае это часть столбца В с адресами из диапазона B2:B7.

Точно так же заполняют поле «Известные значения _ x» и нажимают на кнопку «Ок».

В результате в выделенной ячейке C1 отображается значение 176, являющееся итогом процедуры интерполяции.