Перевод периодической дроби в обыкновенную дробь

Определение периодической дроби

Периодическая дробь — это бесконечная десятичная дробь, в которой, начиная с некоторого места, периодически повторяется определенная группа цифр.

Периодическая часть дроби — это набор повторяющихся цифр, из которых состоит значащая часть.

В краткой записи периодической дроби повторяющиеся цифры пишут в скобках и называют периодом дроби. Например, вместо 1,555… записывают 1,(5) и читают «одна целая и пять в периоде».

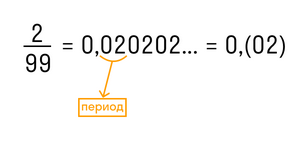
Остальной отрезок значащей части, который не повторяется, называется непериодической частью.

Виды периодических дробей: чистые и смешанные.

Чистая периодическая десятичная дробь — это десятичная дробь, в записи которой сразу после запятой следует период. Например: 1,(4); 4,(25); 21,(693).

Смешанная периодическая десятичная дробь — это десятичная дробь, в записи которой после запятой через одну или несколько цифр начинается период. Например: 3,5(1); 0,02(89); 7,0(123) и т.д.

Рассмотрим примеры дробей, чтобы научиться определять части и период.

1/3 = 0,3333… = 0,(3)

Непериодическая часть: 0; периодическая часть: 3; длина периода: 1.

Читаем так: ноль целых три в периоде.

7/12 = 0,583333… = 0,58(3)

Непериодическая часть: 0,58; периодическая часть: 3; длина периода: снова 1.

Читаем так: ноль целых пятьдесят восемь сотых и три в периоде.

17/11 = 1,545454… = 1,(54)

Непериодическая часть: 1; периодическая часть: 54; длина периода: 2.

Читаем так: одна целая пятьдесят четыре сотых в периоде.

25/39 = 0,641025 641025… = 0,(641025)

Непериодическая часть: 0; периодическая часть: 641025; длина периода: 6.

Читаем так: ноль целых шестьсот сорок одна двадцать пять миллионных в периоде.

пятьдесят четыре сотых в периоде.

9200/3 = 3066,666… = 3066,(6)

Непериодическая часть: 3066; периодическая часть: 6; длина периода: 1.

Читаем так: три тысячи шестьдесят шесть целых и шесть в периоде.

Важные определения

Десятичные дроби

Десятичные дроби можно разделить на две большие группы: конечные и бесконечные десятичные дроби. Десятичные дроби с конечным числом цифр после десятичной точки называются конечными, поскольку в какой-то момент они заканчиваются. Напротив, десятичные дроби с бесконечным числом цифр после запятой называются бесконечными. Эти бесконечные дроби можно разделить на две группы: периодические и непериодические. Если некоторые цифры после запятой бесконечно повторяются, то такое число называется периодической десятичной дробью. Примерами таких десятичных дробей являются:

$$16,3333333\ldots=16,\bar{3}$$

или

$$3,961961961\ldots=3,\bar{961}$$

Бесконечные десятичные дроби, где каждая цифра после запятой разная, называются непериодическими десятичными дробями. Такие числа никогда нельзя выписать полностью. Поэтому использовать их в качестве исходных данных для перевода десятичных дробей в дробные невозможно. Примером неповторяющейся десятичной дроби является:

$$6,7102984637\ldots$$

Дроби и смешанные числа

Конвертер десятичной дроби в дробь переводит заданное десятичное число в дробную или смешанную форму. В дробной форме калькулятор всегда использует правильную дробь — дробь, представляющую число меньше 1, то есть числитель будет меньше знаменателя. Примерами правильных дробей являются:

$$\frac{4}{9}\ или \ \frac{3}{7}$$

Мы называем дробь неправильной, если она представляет собой число, большее или равное 1, то есть числитель будет больше или равен знаменателю. Примерами неправильных дробей являются:

$$\frac{11}{7}\ или \ \frac{13}{2}$$

Если число состоит из целого числа и правильной дроби, оно называется смешанным числом. Примерами смешанных чисел являются:

$$3\frac{3}{5}\ или \ 6\frac{17}{31}$$

Калькулятор выдаст ответ либо в виде правильной дроби, либо в виде смешанного числа.

Получаем периодическую дробь

Попробуем разделить 1 на 3. Не будем подробно останавливаться на том, как это сделать. Этот момент подробно описан в уроке действия с десятичными дробями, в теме деление меньшего числа на большее. Продвинутый уровень.

Итак, делим 1 на 3

Видно, что мы постоянно получаем остаток 1, далее приписываем к нему 0 и делим 10 на 3. И это повторяется вновь и вновь. В результате в дробной части каждый раз получается цифра 3. Деление 1 на 3 будет выполняться бесконечно, поэтому разýмнее будет остановиться на достигнутом.

Такие дроби называют периодическими, поскольку у них присутствует период цифр, который бесконечно повторяется. Период цифр может состоять из нескольких цифр, а может состоять из одной как в нашем примере.

В примере, который мы рассмотрели выше, период в дроби 0,33333 это цифра 3. Обычно такие дроби записывают сокращённо. Сначала записывают цéлую часть, затем ставят запятую и в скобках указывают период (цифру, которая повторяется).

В нашем примере повторяется цифра 3, она является периодом в дроби 0,33333. Поэтому сокращённая запись будет выглядеть так:

0, (3)

Читается как «ноль целых и три в периоде»

Пример 2. Разделить 5 на 11

Это тоже периодическая дробь. Период данной дроби это цифры 4 и 5, эти цифры повторяются бесконечно. Сокращённая запись будет выглядеть так:

0, (45)

Читается как «ноль целых и сорок пять в периоде»

Пример 3. Разделить 15 на 13

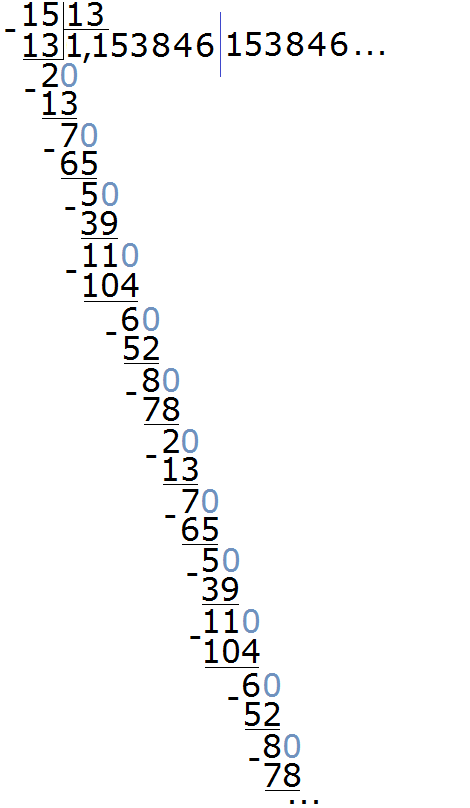
Здесь период состоит из нескольких цифр, а именно из цифр 153846. Для наглядности период отделён синей линией. Сокращённая запись для данной периодической дроби будет выглядеть так:

1, (153846)

Читается как: «одна целая сто пятьдесят три тысячи восемьсот сорок шесть в периоде».

Пример 4. Разделить 471 на 900

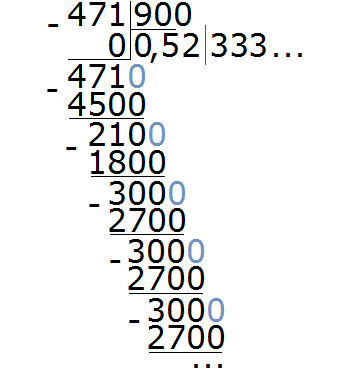
В этом примере период начинается не сразу, а после цифр 5 и 2.  Сокращённая запись для данной периодической дроби будет выглядеть так:

0, 52 (3)

Читается как: «ноль целых пятьдесят две сотых и три в периоде».

Что такое периодическая дробь

Рассматриваемая здесь десятичная дробь относится к классу бесконечных. Существует также и бесконечная непериодическая: например, когда имеем дело с числами типа 0.121231234…, 0.787887888… и т.д.

В общем случае периодической дробью называют бесконечную десятичную, у которой после какого–то знака в числе цифры начинают повторяться, и таким образом прослеживается некая их группа. Собственно, эти самые повторяющиеся цифры являются так называемой значащей (либо просто периодической) частью дроби.

Когда делают краткую запись подобной дроби, цифры, которые повторяются в бесконечном числе, берут в скобки. Это и называют периодом дроби.

ПРИМЕР №1

Дано следующее бесконечно число: 0.1(6). Здесь (6) означает, что после 1 цифра 6 начнёт повторяться, т.е. будет 0.1666…

Введём в соответствующее поле нашего калькулятор периодической дроби в простую  заданное значение (т.е. 0.1(6) – заданное в примере бесконечное число) и получим искомый ответ, т.е. 1/6

ПРИМЕР №2

Дано бесконечное число: 0.(09). Здесь (09) означает, что после точки цифры 0 и 9 начнут повторяться, т.е. будет 0.090909…

Введём в соответствующее поле нашего калькулятора заданное значение и получим искомый ответ, т.е. 1/11

ПРИМЕР №3

Дано бесконечное число: 0.(641025). Здесь период уже более длинный, т.е. 641025.

Введём в соответствующее поле нашего калькулятора заданное значение и получим искомый ответ, т.е. 25/39

Обыкновенные дроби. Деление с остатком

Если нам нужно разделить 497 на 4, то при делении мы увидим, что 497 не делится на 4 нацело, т.е. остаётся остаток от деления. В таких случаях говорят, что выполнено деление с остатком, и решение записывают в таком виде: 497 : 4 = 124 (1 остаток).

Компоненты деления в левой части равенства называют так же, как при делении без остатка: 497 — делимое, 4 — делитель. Результат деления при делении с остатком называют неполным частным. В нашем случае это число 124. И, наконец, последний компонент, которого нет в обычном делении, — остаток. В тех случаях, когда остатка нет, говорят, что одно число разделилось на другое без остатка, или нацело. Считают, что при таком делении остаток равен нулю. В нашем случае остаток равен 1.

Остаток всегда меньше делителя.

Проверку при делении можно сделать умножением. Если, например, имеется равенство 64 : 32 = 2, то проверку можно сделать так: 64 = 32 * 2.

Частное от деления натуральных чисел можно записать в виде дроби.

Числитель дроби — это делимое, а знаменатель — делитель.

Поскольку числитель дроби — это делимое, а знаменатель — делитель, считают, что черта дроби означает действие деление. Иногда бывает удобно записывать деление в виде дроби, не используя знак «:».

Частное от деления натуральных чисел m и n можно записать в виде дроби \( \frac\), где числитель m — делимое, а знаменатель п — делитель: \( m:n = \frac\)

Верны следующие правила:

Чтобы получить дробь \( \frac\), надо единицу разделить на n равных частей (долей) и взять m таких частей.

Чтобы получить дробь \( \frac\), надо число m разделить на число n.

Чтобы найти часть от целого, надо число, соответствующее целому, разделить на знаменатель и результат умножить на числитель дроби, которая выражает эту часть.

Чтобы найти целое по его части, надо число, соответствующее этой части, разделить на числитель и результат умножить на знаменатель дроби, которая выражает эту часть.

Если и числитель, и знаменатель дроби умножить на одно и то же число (кроме нуля), величина дроби не изменится: \( \large \frac = \frac \)

Если и числитель, и знаменатель дроби разделить на одно и то же число (кроме нуля), величина дроби не изменится: \( \large \frac = \frac \) Это свойство называют основным свойством дроби.

Два последних преобразования называют сокращением дроби.

Если дроби нужно представить в виде дробей с одним и тем же знаменателем, то такое действие называют приведением дробей к общему знаменателю.

Избавляемся от хвоста

Подобно тому, как ящерица избавляется от хвоста, мы можем избавить периодическую дробь от повторяющегося периода. Для этого достаточно округлить эту периодическую дробь до нýжного разряда.

Например, округлим периодическую дробь 0, (3) до разряда сотых. Чтобы увидеть сохраняемую и отбрасываемую цифру, временно запишем дробь 0, (3) не в сокращённом виде, а в полном:

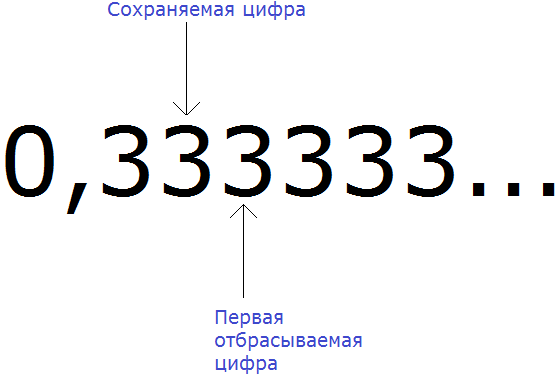
Вспоминаем правило округления. Если при округлении чисел первая из отбрасываемых цифр 0, 1, 2, 3 или 4, то сохраняемая цифра остаётся без изменений.

Значит периодическая дробь 0, (3) при округлении до сотых обращается в дробь 0,33

0, (3) ≈ 0,33

Округлим периодическую дробь 6,31 (6) до разряда тысячных.

Запишем эту дробь в полном виде, чтобы увидеть сохраняемую и отбрасываемую цифру:

Вспоминаем правило округления. Если при округлении чисел первая из отбрасываемых цифр 5, 6, 7, 8 или 9, то сохраняемая цифра увеличивается на единицу.

Значит периодическая дробь 6,31 (6) при округлении до тысячных обращается в дробь 6,317

6,31 (6) ≈ 6,317

Перевод обыкновенных дробей в конечные и бесконечные периодические десятичные дроби

В десятичную дробь можно перевести не только обыкновенные дроби со знаменателями $10, 100, \dots$.

В некоторых случаях исходную обыкновенную дробь можно легко привести к знаменателю $10$, $100$ или $1 \ 000$, после чего можно полученную дробь представить в виде десятичной дроби.

Пример 5

Чтобы дробь $\frac{3}{5}$ }привести к дроби со знаменателем $10$, нужно числитель и знаменатель дроби умножить на $2$, после чего получим $\frac{6}{10}$, которую не составит труда перевести в десятичную дробь $0,6$.

Для остальных случаев используется другой способ перевода обыкновенной дроби в десятичную}:

• числитель нужно заменить десятичной дробью с любым числом нулей после десятичной запятой;

• разделить числитель дроби на знаменатель (деление выполняется как деление натуральных чисел в столбик, а в частном ставят десятичную запятую после окончания деления целой части делимого).

Пример 6

Перевести обыкновенную дробь $\frac{621}{4}$ в десятичную дробь.

Решение.

Число $621$ в числителе представим в виде десятичной дроби. Для этого добавим десятичную запятую и для начала два нуля после нее. Далее при необходимости можно буде добавить нули еще. Итак, получили $621,00$.

Выполним деление числа $621,00$ на $4$ в столбик:

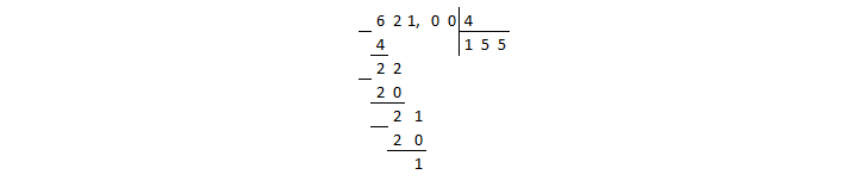Рисунок 1.

Деление дошло до десятичной запятой в делимом, а остаток при этом получили не нулевой. В таком случае в частном ставится десятичная запятая и продолжается деление столбиком, не взирая на запятые:

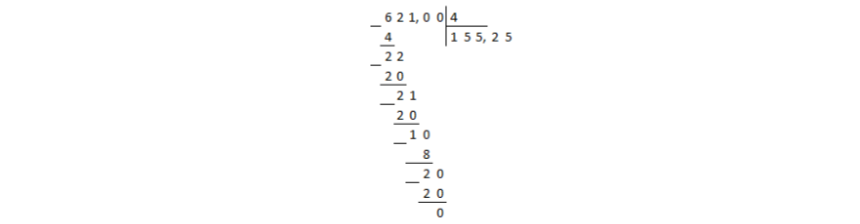Рисунок 2.

В остатке получили нуль, значит деление окончено.

Ответ: $155,25$.

Возможен случай, когда при делении числителя и знаменателя обыкновенной дроби в остатке $0$ так и не получается. В этом случае деление можно продолжать бесконечно. Начиная с определенного момента остатки от деления периодически повторяются, а значит повторяются и цифры в частном. Из этого можно сделать вывод, что данная обыкновенная дробь переведется в бесконечную периодическую десятичную дробь.

Пример 7

Перевести обыкновенную дробь $\frac{19}{44}$ в десятичную дробь.

Решение.}

Для перевода обыкновенной дроби в десятичную выполним деление в столбик:

Рисунок 3.

При делении повторяются остатки $8$ и $36$, а в частном также повторяются цифры $1$ и $8$. Итак, исходную обыкновенную дробь $\frac{19}{44}$ перевели в периодическую дробь $\frac{19}{44}=0,43181818\dots =0,43(18)$.

Ответ: $0,43(18)$.

Общий вывод о переводе обыкновенных дробей в десятичные:

• если знаменатель можно разложить на простые множители, среди которых будут присутствовать только числа $2$ и $5$, то такую дробь можно перевести в конечную десятичную дробь;

• если кроме чисел $2$ и $5$ в разложении знаменателя присутствуют другие простые числа, то такая дробь переводится в бесконечную десятичную периодическую дробь.

Арифметические действия с обыкновенными дробями

Сложение и вычитание дробей

При сложении (вычитании) дробей с одинаковыми знаменателями к числителю первой дроби прибавляют числитель второй дроби (из числителя первой вычитают числитель второй) и оставляют тот же знаменатель. Полученную дробь, если возможно, сокращают и выделяют целую часть.

При сложении (вычитании) дробей с разными знаменателями нужно предварительно привести эти дроби к наименьшему общему знаменателю, затем  сложить (вычесть) полученные дроби, используя правило сложения (вычитания) дробей с одинаковыми знаменателями.

Особенно надо быть внимательным при сложении (вычитании) с участием смешанных чисел!

Общий случай сложения (вычитания) дробей.

 Умножение дробей

1. Произведение двух дробей a/b и c/d равно дроби, числитель которой равен произведению числителей, а знаменатель — произведению знаменателей:
2. При умножении чисел, состоящих из целой и дробной частей, их предварительно представляют в виде неправильных дробей, а затем умножают согласно п. 1.

 Деление дробей

Два числа называются взаимно обратными, если их произведение равно 1, то есть дроби вида a/b и b/a являются взаимно обратными. Например 1/3 и 3. Чтобы разделить одну дробь на другую, нужно делимое умножить на число, обратное к делителю.

При делении чисел, состоящих из целой и дробной части, нужно предварительно представить их в виде неправильной дроби.

Правильные и неправильные дроби, определения, примеры

В основе разделения дробей на правильные и неправильные лежит сравнение числителя и знаменателя в пределах одной дроби.

Определение 7

Правильная дробь – это обыкновенная дробь, в которой числитель меньше, чем знаменатель. Т.е., если выполняется неравенство m < n, то обыкновенная дробь mn является правильной.

Неправильная дробь — это обыкновенная дробь, числитель которой больше или равен знаменателю. Т.е., если выполняется неравенство undefined, то обыкновенная дробь mn является неправильной.

Приведем примеры: — правильные дроби:

Пример 1

59, 367, 138514;

— неправильные дроби:

Пример 2

1313, 573, 901112, 167.

Также возможно дать определение правильных и неправильных дробей, опираясь на сравнение дроби с единицей.

Определение 8

Правильная дробь – обыкновенная дробь, которая меньше единицы.

Неправильная дробь – обыкновенная дробь, равная или бОльшая единицы.

Например, дробь 812 – правильная, т.к. 8 12< 1. Дроби 532 и 1414 являются неправильными, т.к. 532 > 1, а 1414 = 1.

Немного углубимся в размышление, почему дроби, в которых числитель больше или равен знаменателю получили название «неправильных».

Рассмотрим неправильную дробь 88: она сообщает нам, что взято 8 долей предмета, состоящего из 8 долей. Таким образом, из имеющихся восьми долей мы можем составить целый предмет, т.е. заданная дробь 88 по сути представляет целый предмет: 88=1. Дроби, в которых числитель и знаменатель равны, полноценно заменяет натуральное число 1.

Рассмотрим также дроби, в которых числитель превосходит знаменатель: 115 и 363. Понятно, что дробь 115 сообщает о том, что из нее мы можем составить два целых предмета и еще останется одна пятая доля. Т.е. дробь 115 – это 2 предмета и еще 15 от него. В свою очередь, 363 – дробь, означающая по сути 12 целых предметов.

Указанные примеры дают возможность сделать вывод, что неправильные дроби возможно заменить натуральными числами (если числитель без остатка делится на знаменатель: 88 = 1; 363 = 12) или суммой натурального числа и правильной дроби (если числитель не делится на знаменатель без остатка: 115 = 2 + 15). Вероятно, потому такие дроби и получили название «неправильных».

Здесь также мы сталкиваемся с одним из важнейших навыков работы с числами.

Определение 9

Выделение целой части из неправильной дроби – это запись неправильной дроби в виде суммы натурального числа и правильной дроби.

Также отметим, что существует тесная взаимосвязь между неправильными дробями и смешанными числами.

25 thoughts on “Периодические дроби”

Когда же следующие уроки? Уже что-то долго ничего нету

Большое спасибо за урок! Откровенно говоря…эту тему не помню вообще…Будто ее и не было в школе О__о Ну или я ее проболела… (Перевод смешанной периодической дроби в обыкновенную дробь)

Вы бы хоть номер кошелька написали. А то столько трудились и никакой отдачи. С такими уроками никакой экзамен не страшен.

Спасибо большое Тэла, за столь добрый отзыв Если люди получают пользу от этих уроков — это уже отдача)

Огромное Вам спасибо за уроки! Всё объясняете доступно и наглядно! На ваших уроках готовлюсь поступать на ФИТ на программиста. Хорошо бы еще алгебру выложили.)

Вы не могли бы объяснить логику алгоритма перевода периодической дроби в обычную?

Зачем в знаменателе ставятся девятки — заместно, например, округления числа, подставляемого в числитель, до последней цифры периода, и постановки степени 10 в знаменатель? Зачем, при переводе смешанной периодической дроби, производится соотв. вычитание и чем объясняется подстановка нулей и единиц в зависимости от принадлежности цифры к периоду??…

Спасибо большое за урок Скажите пожалуйсто при округлении(когда избавляемся от хвоста) откуда знать до каких разряд надо округлять?

Вот и здесь последняя задача говорит округлить до разряда сотых,а почему не до десятых(например)?

зависит от задачи, которую решаете. Если в задаче сказано округлять до десятых, значит округляете до десятых. Если сказано округлять до сотых — округляете до сотых

Преобразование десятичных дробей в дроби для бесконечных периодических десятичных дробей

Чтобы преобразовать повторяющуюся десятичную дробь в простую дробь, выполните следующие действия.

Напишите уравнение, в котором переменная (например, x) равна десятичному числу с повторяющимися цифрами после запятой, включенными только один раз. Например, если у вас есть десятичное число \$5,61111\ldots=5,6\bar{1}\$, уравнение должно выглядеть следующим образом:

$$x=5,6\bar{1}$$

Определите количество цифр в повторяющейся десятичной группе (n) и умножьте обе стороны уравнения на \${10}^n\$. В нашем случае есть только одна повторяющаяся цифра: 1. Поэтому обе стороны уравнения нужно умножить на \${10}^1=10\$:

$$10x=56,1\bar{1}$$

Вычтите первое уравнение из второго. В нашем примере мы получаем:

$$10x=56,1\bar{1}$$

$$x=5,6\bar{1}$$

$$9x=50,5$$

Проводя вычисления для x, мы получаем:

$$x=\frac{50,5}{9}$$

Чтобы избавиться от десятичных знаков, умножьте числитель и знаменатель числа на 10 в степени n, где n — количество цифр после запятой. В нашем случае после запятой стоит только одна цифра — 5. Поэтому нам нужно умножить на 10:

$$\frac{50,5}{9}×\frac{10}{10}=\frac{505}{90}$$

Найдите наибольший общий коэффициент числителя и знаменателя полученной дроби и уменьшите дробь, разделив числитель и знаменатель на GCF. В нашем случае GCF равен 5, поэтому:

$$\frac{505\div5}{90\div5}=\frac{101}{18}$$

Упростите неправильную дробь:

$$\frac{101}{18}=5\frac{11}{18}$$

В итоге, \$5,6\bar{1}=5\frac{11}{18}\$.

Действия с правильными дробями, как найти

Правильные дроби можно встретить при решении множества задач по математике. Для них предусмотрены все действия, которые выполняют с обыкновенными дробями.

Приведение к общему знаменателю

Перед тем, как сравнить, сложить или вычесть дроби, требуется выполнить их преобразование. В результате арифметических действий дроби должны пробрести одинаковые знаменатели. К примеру, имеется пара дробей:

ab

cd

Последовательность операций:

1. Найти минимальное единое кратное для знаменателей: M=b,d.
2. Умножить числитель и знаменатель первой дроби на Mb.
3. Умножить числитель и знаменатель второй дроби на Md.

В результате знаменатели первой и второй дроби становятся одинаковыми и равными M. Допустимо заменить минимальное единое кратное при решении несложных примеров на какое-либо другое общее кратное. К примеру, таким кратным может стать произведение знаменателей.

Сравнение

С целью сравнения пары обыкновенных дробей необходимо выполнить операцию приведения их к единому знаменателю. Далее следует сравнить числители дробей, которые в итоге получились. Если числитель больше, то и дробь считается больше.

Сложение и вычитание

Прибавить одну обыкновенную дробь к другой обыкновенной дроби можно. Но перед этим требуется выполнить приведение этих дробей к единому знаменателю. После такой операции находят сумму числителей, а знаменатели оставляют без изменений.

При умножении двух обыкновенных дробей требуется выполнить умножение их числителей и знаменателей:

ab·cd=acbd

Возведение в степень и извлечение корня

Дроби можно возводить в степень. При этом необходимо выполнить арифметическое действие возведения в степень отдельно со знаменателем и числителем этой дроби:

abn=anbn,b≠.

Перевод других видов дробей в правильную форму

Для того чтобы перевести неправильную дробь в правильную, либо для выполнения обратного действия, требуется соблюдать определенный порядок. Прямой перевод невозможен. Результатом подобной операции будет являться преобразованная запись, которая содержит в себе целую, а также дробную части. Последовательность действий:

• упростить запись дробного отношения;
• вычислить произведение целой части и делителя дробной части;
• сложить результата умножения с числителем;
• полученную сумму записать в качестве делимого преобразованного выражения;
• знаменатель нужно оставить прежним.

С помощью достаточно простого метода удобно переводить числа из одной формы в какую-либо другую. Данный алгоритм можно записать в виде математического уравнения:

na÷b=((n×b)+a)÷b

Смешанное отношение представляет собой сумму из целого и части. Для того чтобы понять, как преобразовать дроби, следует выполнить сложение в качестве арифметического действия.  В процессе первое слагаемое нужно записать в виде неправильной дроби путем деления целого на 1. Далее целесообразно воспользоваться правилом сложения дробей. Выполняется поиск общего знаменателя, дополнительных множителей, сложение в числителе. Формула имеет такой вид:

na÷b=n÷1+a÷b=((n×b)+a)÷b

Неправильную дробь превратить в обычную можно с помощью перевода ее в смешанную. В процессе выражение записывают в виде суммы натурального числа и правильной дроби:

1. Найти отношение делимого к делителю.
2. Полученный результат записать в числителе.
3. Знаменатель будет равен исходному числу, стоящему в делителе.
4. Приписать частное к выражению в виде целой доли.

Более простой способ преобразования дробей заключается в представлении делимого, как суммы дробей

При этом важно, чтобы при делении одной из них не было остатка:. m÷n=(k+c)÷n=k÷n+c÷n. m÷n=(k+c)÷n=k÷n+c÷n

m÷n=(k+c)÷n=k÷n+c÷n

Здесь целое число k÷n, а c÷n является правильной дробью.

1.5.1. Выбор типа дроби и картечи

1.5.1. Выбор типа дроби и картечи

Свинцовая дробь в зависимости от содержания в ней сурьмы и соединений мышьяка производится следующих типов: охотничья твердая (ОТ); охотничья мягкая (ОМ); спортивная твердая (СТ). По способу изготовления дробь может быть штампованной (Ш), литой (Л), катанной (К). В зависимости от норм отклонений диаметров при изготовлении и норм твердости дробь разделяется на первую и высшую категории качества.

В настоящее время охотничья мягкая дробь (ОМ) и картечь (КО) производятся из почти чистого свинца и имеют твердость 5–6 кг/мм?. Твердая дробь должна быть тверже более чем в два раза — до 13–16 кг/мм?.

Мягкая дробь из чистого свинца значительно деформируется при выстреле; периферийные дробины, двигаясь по снарядному входу патронника и каналу ствола, значительно истираются, теряя форму и примерно половину массы, что ухудшает выстрел.

В послевоенные годы, для уменьшения свинцевания канала ствола и предупреждения отравления дичи свинцом, твердую дробь стали покрывать гальваническим способом тонким слоем меди, никеля или хрома. Такая дробь (ее иногда именуют плакированной) меньше деформируется при движении по каналу ствола, что позволяет увеличить ее начальную скорость.

В разное время и в разных странах неоднократно предпринимались попытки изготовить дробь не из свинца, а из других металлов (железа, чугуна), но все они оканчивались неудачей, так как бой ружья дробью из заменителей был хуже по сравнению с боем обычной свинцовой дробью. В СШАдовольно широко применяют стальную дробь; при этом процент раненых, но не взятых птиц резко возрастает.

Правильная шарообразная форма, одинаковый диаметр и вес дроби обеспечивают снаряду при выстреле компактный полет и меньшую растянутость, что и определяет качество выстрела. В связи с этим следует отметить, что размер и качество дроби, поступающей в продажу, в значительной степени не соответствует требованиям, согласно которым обычная литая дробь должна быть круглой с допуском по диаметру в пределах + 0,12 мм, а спортивная дробь, предназначенная для стендовых соревнований, изготовляется с отклонениями по размеру ± 0.1 мм. В торговой же расфасовке дробь мелкого размера практически всегда имеет некруглую форму и много сдвоенных дробин; более крупная дробь напоминает скорее грушу или чечевицу с раковинами и свищами на поверхности, при этом диаметр отдельных дробин резко отличается друг от друга.

Деформированная дробь при вылете из канала ствола ружья ведет себя в воздухе подобно брошенному плоскому камню: она косо отклоняется от основного направления выстрела и, кроме того, теряет скорость гораздо быстрее, чем круглая дробина. Отклонение от центра на 35 м может достигать 2 м и более. Поэтому при тщательном снаряжении патронов такую дробь, особенно первые и нулевые номера, стрелку приходится предварительно прокатывать для придания ей сферической формы, а для получения дроби одного размера и веса ее откалибровывают, просевая через сито. Наиболее перспективным является метод изготовления дроби точной штамповкой, так как штампованная дробь обладает более правильной формой и меньшей разномерностью, чем литая.

Казалось бы, все ясно, необходимо применять только твердую дробь, чтобы максимально использовать возможности дробового выстрела. Однако приобрести патроны, снаряженные твердой дробью, или саму твердую дробь практически нельзя. Наша промышленность многие десятилетия выпускала и выпускает в основном мягкую дробь и картечь. Это делается потому, что в технологическом отношении выпускать мягкую дробь и картечь проще и производительнее.

Многолетняя стрельба мягкой дробью привела к тому, что из-за неэффективности выстрела многие охотники стали применять дробь на несколько номеров более крупную, чем это необходимо для определенной дичи. При такой дроби в снаряде размещается меньше дробин, в дичь на нормальной дистанции попадают лишь одна-две дробины, и она часто погибает вне пределов досягаемости охотника.

Как показали измерения твердости дроби производства иностранных фирм, эта дробь имеет среднюю твердость 15 кг/мм?. Измерения твердости картечи и «Ремингтон» показали, что она имеет твердость в среднем 9 кг/мм?. Во время испытаний патроны с картечью и «Ремингтон» показали в среднем до 15 % большую кучность и до 25 % большую пробиваемость, чем аналогичные патроны отечественного производства.

Перевод смешанной периодической дроби в обыкновенную дробь

Чтобы перевести смешанную периодическую дробь в обыкновенную дробь, нужно в числителе записать разность в которой уменьшаемое это цифры, стоящие после запятой в периодической дроби, а вычитаемое — цифры, стоящие между запятой и первым периодом периодической дроби.

В знаменателе же нужно записать некоторое количество девяток и нулей. При этом, количество девяток должно быть равно количеству цифр в периоде периодической дроби, а количество нулей должно быть равно количеству цифр между запятой и периодом периодической дроби.

Например, переведём смешанную периодическую дробь 0,31 (6) в обыкновенную дробь.

Сначала запишем в числителе разность. Уменьшаемым будут все цифры, стоящие после запятой (включая и период), а вычитаемым будут цифры, стоящие между запятой и периодом:

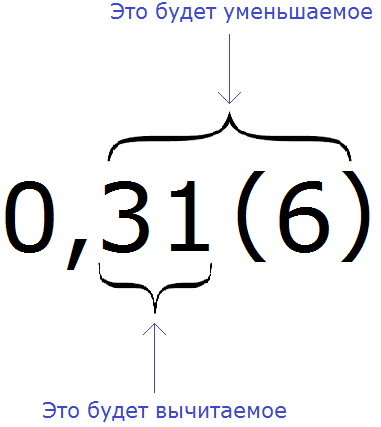
Итак, записываем в числителе разность:

А в знаменателе запишем некоторое количество девяток и нулей. Количество девяток должно быть равно количеству цифр в периоде периодической дроби 0,31 (6)

В дроби 0,31 (6) период состоит из одной цифры. Значит в знаменатель дроби записываем одну девятку:

Теперь дописываем количество нулей. Количество нулей должно быть равно количеству цифр между запятой и периодом периодической дроби.

В дроби 0,31 (6) между запятой и периодом располагается две цифры. Значит в знаменателе дроби должно быть два нуля. Дописываем их:

Получили выражение, которое вычисляется легко:

Получили ответ

Таким образом, при переводе периодической дроби 0,31 (6) в обыкновенную дробь, получается

Пример 2. Перевести смешанную периодическую дробь 0,72 (62) в обыкновенную дробь

Сначала запишем в числителе разность. Уменьшаемым будут все цифры, стоящие после запятой (включая и период), а вычитаемым будут цифры, стоящие между запятой и периодом:

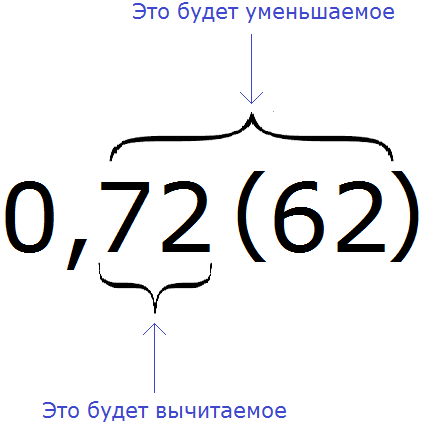
Итак, записываем в числителе разность:

А в знаменателе запишем некоторое количество девяток и нулей. Количество девяток должно быть равно количеству цифр в периоде периодической дроби 0,72 (62)

В дроби 0,72 (62) период состоит из двух цифр. Значит в знаменатель дроби записываем две девятки:

Теперь дописываем количество нулей. Количество нулей должно быть равно количеству цифр между запятой и периодом периодической дроби.

В дроби 0,72 (62) между запятой и периодом располагаются две цифры. Значит в знаменателе дроби должно быть два нуля. Дописываем их:

Получили выражение, которое вычисляется легко:

Получили ответ

Значит при переводе периодической дроби 0,72 (62) в обыкновенную дробь, получается

Понравился урок? Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Возникло желание поддержать проект? Используй кнопку ниже