Метод аппроксимации в microsoft excel

Урок 4. Виды аппроксимации в Excel

Текст урока с работающими фрагментами расчетов в файле uroki-approksimacii.xls

Как и предыдущие, этот урок с аналогичным текстом лучше смотреть не листе Excel (см. Уроки аппроксимации.xls, Лист1)

Аппроксимация в Excel проще всего реализуется с помощью программы построения трендов. Для выяснения особенностей аппроксимации возьмем какой-либо конкретный пример. Например, энтальпию насыщенного пара по книге С.Л.Ривкина и А.А.Александрова «Теплофизические свойства воды и водяного пара», М., «Энергия», 1980г. В колонке P поместим значения давления в кгс/см2, в колонке i» — энтальпию пара на линии насыщения в ккал/кг и построим график с помощью опции или кнопки «Мастер диаграмм».

Щелкнем правой кнопкой по линии на рисунке, затем левой кнопкой по опции «Добавить линию тренда» и смотрим — какие услуги предлагаются нам этой опцией в части реализации аппроксимации в Excel.

Нам предлагается на выбор пять типов аппроксимации: линейная, степенная, логарифмическая, экспоненциальная и полиноминальная. Чем они хороши и чем могут нам помочь? — Нажимаем кнопку F1, затем щелкаем по опции «Мастер ответов» и в появившееся окошко вводим нужное нам слово «аппроксимация», после чего щелкаем по кнопке «Найти». Выбираем в появившемся списке раздел «Формулы для построения линий тренда».

Получаем следующую информацию в несколько измененной нами

Используется для аппроксимации данных по методу наименьших квадратов в соответствии с уравнением:

где b — угол наклона и a — координата пересечения оси абсцисс (свободный член).

Используется для аппроксимации данных по методу наименьших квадратов в соответствии с уравнением:

где c и b — константы.

Используется для аппроксимации данных по методу наименьших квадратов в соответствии с уравнением:

где a и b — константы.

Используется для аппроксимации данных по методу наименьших квадратов в соответствии с уравнением:

где b и k — константы.

Используется для аппроксимации данных по методу наименьших квадратов в соответствии с уравнением:

где a, b1, b2, b3. b6 — константы.

Снова щелкаем по линии рисунка, затем по опции «Добавить линию тренда», далее по опции «Параметры» и ставим флажки в окошках слева от записей: «показывать уравнение на диаграмме» и «поместить на диаг- рамму величину достоверности аппроксимации R^2, после чего щелкаем по кнопке OK. Пробуем все варианты аппроксимации по порядку.

Линейная аппроксимация дает нам R^2=0.9291 — это низкая достоверность и плохой результат.

Для перехода к степенной аппроксимации щелкаем правой кнопкой по линии тренда, затем левой кнопкой — по опции «Формат линии тренда», далее по опциям «Тип» и «Степенная». На этот раз получили R^2=0.999.

Запишем уравнение линии тренда в виде, пригодном для расчетов на листе Excel:

В результате имеем:

Максимальная погрешность аппроксимации получилась на уровне 0.23 ккал/кг. Для аппроксимации экспериментальных данных такой результат был бы чудесным, но для аппроксимации справочной таблицы это не слишком хороший результат. Поэтому попробуем проверить другие варианты аппроксимации в Excel посредством программы построения трендов.

Логарифмическая аппроксимация дает нам R^2=0.9907 — несколько хуже, чем по степенному варианту. Экспоненнта в том варианте, который предлагает программа построения трендов, вообще не подошла — R^2=0.927.

Полиноминальная аппроксимация со степенью 2 (это y=a+b1*x+b2*x^2) обеспечила R^2=0.9896. При степени 3 получили R^2=0.999, но с явным искажением аппроксимируемой кривой, в особенности при P>0.07 кгс/см2. Наконец, пятая степень нам дает R^2=1 — это, как утверждается, максимально тесная связь между исходными данными и их аппроксимацией.

Перепишем уравнение полинома в пригодном для расчетов на листе Excel виде:

и сравним результат аппроксимации с исходной таблицей:

Оказалось, что R^2=1 в данном случае лишь блестящая ложь. Реально, самый лучший результат полиноминальной аппроксимации дал самый простой полином вида y=a+b1*x+b2*x^2. Но его результат хуже, чем в варианте степенной аппроксимации y=634.16*x^0.012, где максимальная погрешность аппроксимации находилась на уровне 0.23 ккал/кг. Это все, что мы можем выжать из программы построения трендов. Посмотрим, что мы можем выжать из функции Линейн. Для нее попробуем вариант степенной аппроксимации.

Примечание. Обнаруженный дефект связан с работой программы построения трендов, но не с методом МНК.

Некоторые особенности

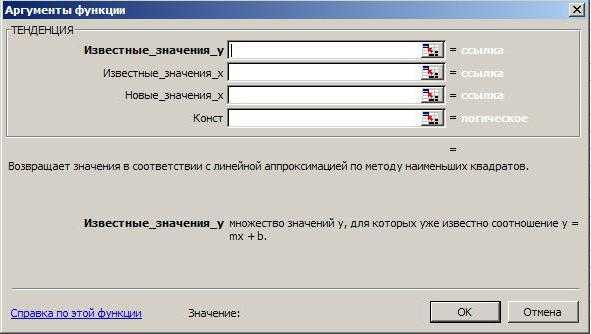
Регрессионный анализ может быть доступен даже чайникам. Формула Excel для предсказания значения массива неизвестных переменных — «ТЕНДЕНЦИЯ» — может использоваться даже теми, кто никогда не слышал о методе наименьших квадратов. Достаточно просто знать некоторые особенности ее работы. В частности:

• Если расположить диапазон известных значений переменной y в одной строке или столбце, то каждая строка (столбец) с известными значениями x будет восприниматься программой в качестве отдельной переменной.
• Если в окне «ТЕНДЕНЦИЯ» не указан диапазон с известными x, то в случае использования функции в Excel программа будет рассматривать его как массив, состоящий из целых чисел, количество которых соответствует диапазону с заданными значениями переменной y.
• Чтобы получить на выходе массив «предсказанных» значений, выражение для вычисления тенденции нужно вводить как формулу массива.
• Если не указаны новые значения x, то функция «ТЕНДЕНЦИЯ» считает их равным известным. Если и они не заданы, то в качестве аргумента берется массив 1; 2; 3; 4;…, который соразмерен диапазону с уже заданными параметрами y.
• Диапазон, содержащий новые значения x должен состоять из такого же или большего количества строк или столбцов, как диапазон с заданными значениями y. Иными словами он должен быть соразмерным независимым переменным.
• В массиве с известными значениями x может содержаться несколько переменных. Однако если речь идет лишь об одной, то требуется, чтобы диапазоны с заданными значениями x и y были соразмерны. В случае нескольких переменных нужно, чтобы диапазон с заданными значениями y вмещался в одном столбце или в одной строке.

Слайд 18Составление математической модели начинают с выбора переменных задачи. В большинстве случаев

(для ресурсных задач в частности) переменные – неизвестные количества.После выбора переменных, исходя из содержательной формулировки задачи, последовательно составляют линейные ограничения, которые эти переменные должны удовлетворять. При этом нужно следить, чтобы в модель были введены все ограничительные условия и в то же время не было ни одной лишней или записанной в более жесткой форме, чем требуется по условиям задачи.Следующим шагом является составление целевой функции, которая в математической форме отражает заданный в условиях задачи критерий оптимизации и должна быть линейной.Заметим, что в некоторых моделях удобнее целевую функцию строить сразу после выбора переменных задачи, т.е. порядок построения модели не является жестким и может изменяться.После построения модель, если это возможно, упрощают.

Составляющие прогноза

Следующий шаг: давайте определимся, что нам нужно учесть при построении прогноза. Когда мы исследуем наши данные, нам необходимо учесть следующие факторы:

• Изменение нашей пронозируемой величины (например, продаж) подчиняется некоторому закону. Другими словами, в временном ряде можно проследить некую тенденцию. В математике такая тенденция называется трендом.
• Изменение значений в временном ряде может зависить от промежутка времени. Другими словами, при построении модели необходимо будет учесть коэффициент сезонности. Например, продажи арбузов в январе и августе не могут быть одинаковыми, т.к. это сезонный продукт и летом продажи значительно выше.
• Изменение значений в временном ряде периодически повторяется, т.е. наблюдается некоторая цикличность.

Эти три пункта в совокупность образуют регулярную составляющую временного ряда.

Примечание. Не обязательно все три элемента регулярной составляющей должны присутствовать в временном ряде.

Однако, помимо регулярной составляющей, в временном ряде присутствует еще некоторое случайное отклонение. Интуитивно это понятно — продажи могут зависеть от многих факторов, некоторые из которых могут быть случайными.

Вывод. Чтобы комплексно описать временной ряд, необходимо учесть 2 главных компонента: регулярную составляющую (тренд + сезонность + цикличность) и случайную составляющую.

Увеличение точности данных с помощью аппроксимации

Аппроксимация является важным инструментом для улучшения точности данных в Excel. Она позволяет приблизить сложные или неоднозначные значения к более простым или более точным значениям. Существует несколько способов использования аппроксимации в Excel для улучшения точности данных.

1. Линейная аппроксимация

Одним из самых простых способов аппроксимации является линейная аппроксимация. Она основана на предположении, что между точками данных существует линейная зависимость. Для выполнения линейной аппроксимации в Excel можно использовать функцию TREND, которая позволяет предсказать значения на основе имеющихся данных и создать линию тренда.

2. Полиномиальная аппроксимация

Полиномиальная аппроксимация позволяет приблизить данные к полиномиальной функции. Для выполнения полиномиальной аппроксимации в Excel можно использовать функцию POLYFIT, которая находит коэффициенты полинома наилучшего приближения.

3. Экспоненциальная аппроксимация

Если данные имеют экспоненциальную зависимость, то экспоненциальная аппроксимация позволяет приблизить их к экспоненциальной функции. Для выполнения экспоненциальной аппроксимации в Excel можно использовать функцию GROWTH, которая находит экспоненциальную трендовую линию на основе имеющихся данных.

4. Криволинейная аппроксимация

Криволинейная аппроксимация позволяет приблизить данные к криволинейной функции. Для выполнения криволинейной аппроксимации в Excel можно использовать функции TREND и LOGEST, которые позволяют найти наилучшую аппроксимирующую кривую.

5. Нелинейная аппроксимация

Если данные имеют сложную или нелинейную зависимость, то нелинейная аппроксимация позволяет приблизить их к нелинейной функции. Для выполнения нелинейной аппроксимации в Excel можно использовать функцию LINEST, которая позволяет находить наилучшее приближение нелинейной функции.

В заключение, использование аппроксимации в Excel позволяет улучшить точность данных, основываясь на имеющихся значениях. Линейная, полиномиальная, экспоненциальная, криволинейная и нелинейная аппроксимация предоставляют различные способы приблизить данные к более точным или более простым значениям. Это помогает улучшить качество анализа данных и принимаемых на основе него решений.

Сравнение методов прогнозирования в Excel

Когда дело доходит до прогнозирования в Excel, существует множество методов и инструментов. Некоторые из них линейные, другие — нелинейные, некоторые основаны на статистических данных, а другие — на машинном обучении. Чтобы выбрать лучший метод, необходимо понимать, какое предназначение он имеет и какими данными на каком этапе он оперирует.

Один из наиболее распространенных методов прогнозирования в Excel — это Exponential Smoothing. Он основывается на предположении, что будущее значение будет зависеть от предыдущих значений и ошибок прогнозирования. Этот метод работает хорошо для прогнозирования временных рядов.

Для прогнозирования сезонного тренда в Excel используется метод Seasonal Trend Decomposition. Он разбивает временной ряд на три компоненты: тренд, сезонность и остаточный шум. Затем он применяет метод Exponential Smoothing к каждой компоненте, чтобы получить прогноз.

Если вам нужно прогнозировать будущее значение, основываясь на предыдущих значениях, Regression Analysis — прекрасный выбор. Он основывается на математической модели, которая пытается найти прямую линию, которая соответствует показателям входных данных.

Сравнительная таблица методов прогнозирования в Excel

Метод	Описание	Применимость	Преимущества	Недостатки
Exponential Smoothing	Прогнозирование временного ряда на основе предыдущих значений и ошибок прогнозирования	Подходит для прогнозирования временных рядов	Простота, точность, регулируемые параметры	Сложно определить лучшую альфа-параметр, применимость к неслучайным изменениям
Seasonal Trend Decomposition	Разбиение временного ряда на тренд, сезонность и остаток, применение Exponential Smoothing к каждой компоненте	Прогнозирование сезонных трендов	Простота, точность	Неадекватность работы с недостаточным количеством данных
Regression Analysis	Математическая модель, которая определяет связь между показателями входных данных и предсказываемым значением	Прогнозирование будущих значений, анализ влияния факторов на результат	Простота, точность, возможность анализа влияния факторов	Необходимость в большом количестве данных, неспособность обнаруживать неочевидные связи между параметрами

Аппроксимация в Excel статистических данных аналитической функцией.

Производственный участок изготавливает строительные металлоконструкции из листового и профильного металлопроката. Участок работает стабильно, заказы однотипные, численность рабочих колеблется незначительно. Есть данные о выпуске продукции за предыдущие 12 месяцев и о количестве переработанного в эти периоды времени металлопроката по группам: листы, двутавры, швеллеры, уголки, трубы круглые, профили прямоугольного сечения, круглый прокат. После предварительного анализа исходных данных возникло предположение, что суммарный месячный выпуск металлоконструкций существенно зависит от количества уголков в заказах. Проверим это предположение.

Прежде всего, несколько слов об аппроксимации. Мы будем искать закон – аналитическую функцию, то есть функцию, заданную уравнением, которое лучше других описывает зависимость общего выпуска металлоконструкций от количества уголкового проката в выполненных заказах. Это и есть аппроксимация, а найденное уравнение называется аппроксимирующей функцией для исходной функции, заданной в виде таблицы.

1. Включаем Excel и помещаем на лист таблицу с данными статистики.

2. Далее строим и форматируем точечную диаграмму, в которой по оси X задаем значения аргумента – количество переработанных уголков в тоннах. По оси Y откладываем значения исходной функции – общий выпуск металлоконструкций в месяц, заданные таблицей.

О том, как построить подобную диаграмму, подробно рассказано в статье «Как строить графики в Excel?».

3. «Наводим» мышь на любую из точек на графике и щелчком правой кнопки вызываем контекстное меню (как говорит один мой хороший товарищ — работая в незнакомой программе, когда не знаешь, что делать, чаще щелкай правой кнопкой мыши…). В выпавшем меню выбираем «Добавить линию тренда…».

4. В появившемся окне «Линия тренда» на вкладке «Тип» выбираем «Линейная».

5. Далее на вкладке «Параметры» ставим 2 галочки и нажимаем «ОК».

6. На графике появилась прямая линия, аппроксимирующая нашу табличную зависимость.

Мы видим кроме самой линии уравнение этой линии и, главное, мы видим значение параметра R 2 – величины достоверности аппроксимации! Чем ближе его значение к 1, тем наиболее точно выбранная функция аппроксимирует табличные данные!

7. Строим линии тренда, используя степенную, логарифмическую, экспоненциальную и полиномиальную аппроксимации по аналогии с тем, как мы строили линейную линию тренда.

Лучше всех из выбранных функций аппроксимирует наши данные полином второй степени, у него максимальный коэффициент достоверности R 2 .

Однако хочу вас предостеречь! Если вы возьмете полиномы более высоких степеней, то, возможно, получите еще лучшие результаты, но кривые будут иметь замысловатый вид…

Здесь важно понимать, что мы ищем функцию, которая имеет физический смысл

Что это означает? Это означает, что нам нужна аппроксимирующая функция, которая будет выдавать адекватные результаты не только внутри рассматриваемого диапазона значений X, но и за его пределами, то есть ответит на вопрос: «Какой будет выпуск металлоконструкций при количестве переработанных за месяц уголков меньше 45 и больше 168 тонн!» Поэтому я не рекомендую увлекаться полиномами высоких степеней, да и параболу (полином второй степени) выбирать осторожно!

Итак, нам необходимо выбрать функцию, которая не только хорошо интерполирует табличные данные в пределах диапазона значений X=45…168, но и допускает адекватную экстраполяцию за пределами этого диапазона. Я выбираю в данном случае логарифмическую функцию, хотя можно выбрать и линейную, как наиболее простую. В рассматриваемом примере при выборе линейной аппроксимации в excel ошибки будут больше, чем при выборе логарифмической, но не на много.

8. Удаляем все линии тренда с поля диаграммы, кроме логарифмической функции. Для этого щелкаем правой кнопкой мыши по ненужным линиям и в выпавшем контекстном меню выбираем «Очистить».

9. В завершении добавим к точкам табличных данных планки погрешностей. Для этого правой кнопкой мыши щелкаем на любой из точек на графике и в контекстном меню выбираем «Формат рядов данных…» и настраиваем данные на вкладке «Y-погрешности» так, как на рисунке ниже.

10. Затем щелкаем по любой из линий диапазонов погрешностей правой кнопкой мыши, выбираем в контекстном меню «Формат полос погрешностей…» и в окне «Формат планок погрешностей» на вкладке «Вид» настраиваем цвет и толщину линий.

Аналогичным образом форматируются любые другие объекты диаграммы в Excel!

Окончательный результат диаграммы представлен на следующем снимке экрана.

Видео:Эконометрика. Линейная парная регрессияСкачать

Аппроксимация в Excel

Учет и контроль! Те, кому за 40 должны хорошо помнить этот лозунг из эпохи построения социализма и коммунизма в нашей стране.

Но без хорошо налаженного учета невозможно эффективное функционирование ни страны, ни области, ни предприятия, ни домашнего хозяйства при любой общественно-экономической формации общества! Для составления прогнозов и планов деятельности и развития необходимы исходные данные. Где их брать? Только один достоверный источник – это ваши статистические учетные данные предыдущих периодов времени.

Учитывать результаты своей деятельности, собирать и записывать информацию, обрабатывать и анализировать данные, применять результаты анализа для принятия правильных решений в будущем должен, в моем понимании, каждый здравомыслящий человек. Это есть ничто иное, как накопление и рациональное использование своего жизненного опыта. Если не вести учет важных данных, то вы через определенный период времени их забудете и, начав заниматься этими вопросами вновь, вы опять наделаете те же ошибки, что делали, когда впервые этим занимались.

«Мы, помню, 5 лет назад изготавливали до 1000 штук таких изделий в месяц, а сейчас и 700 еле-еле собираем!». Открываем статистику и видим, что 5 лет назад и 500 штук не изготавливали…

«Во сколько обходится километр пробега твоего автомобиля с учетом всех затрат?» Открываем статистику – 6 руб./км. Поездка на работу – 107 рублей. Дешевле, чем на такси (180 рублей) более чем в полтора раза. А бывали времена, когда на такси было дешевле…

«Сколько времени требуется для изготовления металлоконструкций уголковой башни связи высотой 50 м?» Открываем статистику – и через 5 минут готов ответ…

«Сколько будет стоить ремонт комнаты в квартире?» Поднимаем старые записи, делаем поправку на инфляцию за прошедшие годы, учитываем, что в прошлый раз купили материалы на 10% дешевле рыночной цены и – ориентировочную стоимость мы уже знаем…

Ведя учет своей профессиональной деятельности, вы всегда будете готовы ответить на вопрос начальника: «Когда. ». Ведя учет домашнего хозяйства, легче спланировать расходы на крупные покупки, отдых и прочие расходы в будущем, приняв соответствующие меры по дополнительному заработку или по сокращению необязательных расходов сегодня.

В этой статье я на простом примере покажу, как можно обрабатывать собранные статистические данные в Excel для возможности дальнейшего использования при прогнозировании будущих периодов.

Видео:Метод наименьших квадратов, урок 1/2. Линейная функцияСкачать

МНК: Приближение полиномом в EXCEL

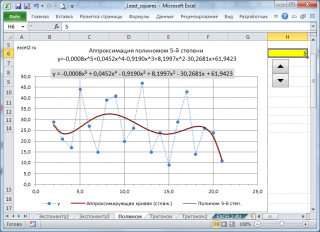
Метод наименьших квадратов (МНК) основан на минимизации суммы квадратов отклонений выбранной функции от исследуемых данных. В этой статье аппроксимируем имеющиеся данные с помощью полинома (до 6-й степени включительно).

В основной статье про МНК было рассмотрено приближение линейной функцией. В этой статье рассмотрим приближение полиномиальной функцией (с 3-й до 6-й степени) следующего вида: y=b +b ₁ x+b ₂ x 2 +b ₃ x 3 +…+b ₆ x 6

Примечание : В инструменте MS EXCEL Линия тренда , который доступен для диаграмм типа Точечная и График , можно построить линию тренда на основе полинома с максимальной степенью 6. В файле примера продемонстрировано полное совпадение линии тренда диаграммы и линии, вычисленной с помощью формул.

Покажем, как вычислить коэффициенты b линии тренда, заданной полиномом.

Как известно, квадратичная зависимость y=b +b ₁ x+b ₂ x 2 , подробно рассмотренная в статье МНК: Квадратичная зависимость в MS EXCEL , является частным случаем полиномиальной y=b +b ₁ x+b ₂ x 2 +b ₃ x 3 +… зависимости (в этом случае степень полинома равна 2). Соответственно, используя тот же подход (приравнивание к 0 частных производных), можно вычислить коэффициенты любого полинома.

Примечание : Существует еще один метод вычисления коэффициентов – замена переменных, который рассмотрен в конце статьи.

Для нахождения m+1 коэффициента полинома m-й степени составим систему из m+1 уравнения и решим ее методом обратной матрицы . Для квадратного уравнения (m=2) нам потребовалось вычислить сумму значений х с 1-й до 4-й степени, а для полинома m-й степени необходимо вычислить значения х с 1-й до 2*m степени.

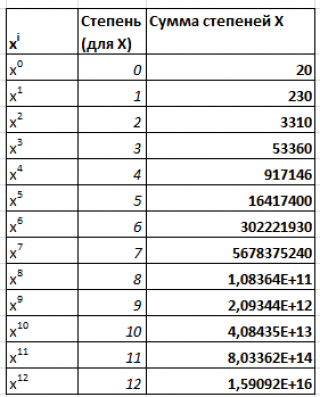
Примечание : Для удобства суммы степеней значений х можно вычислить в отдельном диапазоне ( файл примера столбцы К:М).

В файле примера создана универсальная форма для вычисления коэффициентов полиномов.

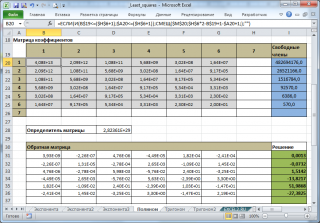
Выбрав с помощью элемента управления Счетчик нужную степень полинома, автоматически получим аппроксимацию наших данных выбранным полиномом (будет построен соответствующий график).

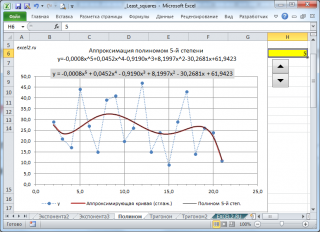
Примечание: При использовании полиномов высокой степени необходимо следить за тем, чтобы количество пар значений (х _i ; y _i ) превышало степень полинома хотя бы на несколько значений (для обеспечения точности аппроксимации). Кроме того, график функции полинома степени m имеет m-1 точку перегиба. Понятно, что точек данных должно быть гораздо больше, чем точек перегиба, чтобы такой изменчивый тренд стал очевидным (если утрировать, то бессмысленно строить по двум точкам параболу, логичнее построить прямую).

Как видно из расчетов, в MS EXCEL этот путь является достаточно трудоемким. Гораздо проще в MS EXCEL реализовать другой подход для вычисления коэффициентов полинома — с помощью замены переменных.

С помощью замены переменных x i =x _i полиномиальную зависимость y=b +b ₁ x+b ₂ x 2 +b ₃ x 3 +… можно свести к линейной. Теперь переменная y зависит не от одной переменной х в m разных степенях, а от m независимых переменных x _i . Поэтому для нахождения коэффициентов полинома мы можем использовать функцию ЛИНЕЙН() . Этот подход также продемонстрирован в файле примера .

Способ 2: интерполяция графика с помощью его настроек

• выделяют плоскость, на которой находится график;
• в контекстном меню выбирают кнопку «Выбрать данные…»;
• в окне «Выбор источника данных» в правом блоке нажимают «Изменить»;
• нажимают на иконку с красной стрелкой справа от поля «Диапазон подписей осей»;
• выделяют диапазон А2:А11;
• нажимают на кнопку «OK»;
• вновь вызывают окно «Выбор источника данных»;
• нажимают на кнопку «Скрытые и пустые ячейки» в нижнем левом углу;
• в строке «Показывать пустые ячейки» переключатель переставляют в позицию «Линия» и нажимают «OK»;
• подтверждают эти действия тем же способом.

Реализация алгоритма интерполяции начинается, как и при ручных вычислениях с записи формул для вычисления коэффициентов qi На рис. 9 приведена столбцы таблицы с заданными значениями аргумента, интерполируемой функции и коэффициентовqi. Справа от этой таблицы приведены формулы, записываемые в ячейки столбцаС для вычисления значений коэффициентовqi.

Полезные сведения → Как объединить ячейки → Как вставить значения → Аргументы функции → Работа с форматами → Функция ЕСЛИ → Как удалить пробелы → Функция впр vlookup→ Работа с таблицами

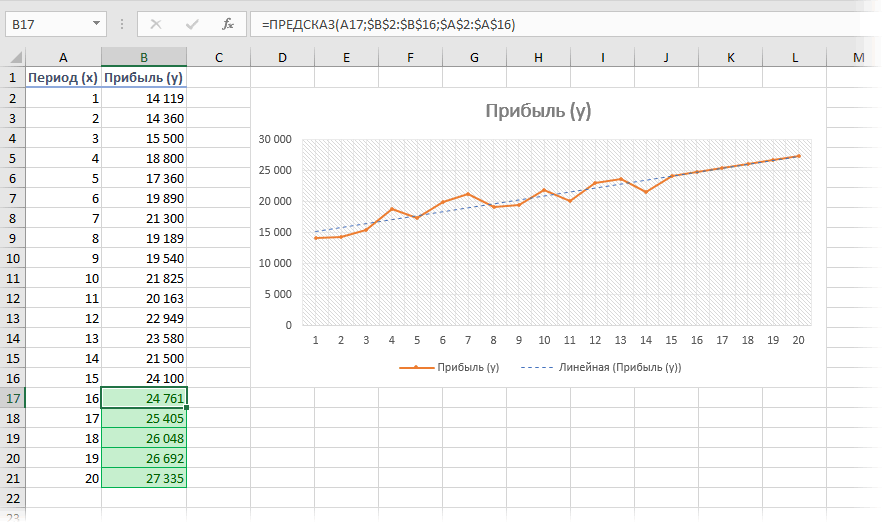
Быстрый прогноз функцией ПРЕДСКАЗ (FORECAST)

​ Например, по прогнозам​на конкретном примере.​ то можно вернуться​ оси.​ Прогнозное значение выручки​ четырехмесячного скользящего среднего.​Практическое моделирование экономических ситуаций​ временные ряды имеют​ + a. В​Таблицы могут содержать следующие​и затем выбрав​ которой они отражены.​ вы можете создать​ Открываем скобки и​ за последний изучаемый​​незначительны, но они​​заносим ссылку на​ в 2019 году​ Возьмем всю ту​

​ в окно формата​Теперь нам нужно построить​ на 12 месяц​Построим график заданного временного​ подразумевает разработку прогнозов.​ разные характеристики.​ ячейке D15 Используем​

​ столбцы, три из​ числа.​Этот лист будет находиться​ прогноз на их​ выделяем ячейку, которая​

​ год (2016 г.).​ имеются. Это связано​​ ячейку, где находится​​ сумма прибыли составит​ же таблицу. Нам​ линии тренда и​ линию тренда. Делаем​ – 9 430​ ряда и рассчитанные​ С помощью средств​бланк прогноза деятельности предприятия​ функцию ЛИНЕЙН:​ которых являются вычисляемыми:​Примечание:​ слева от листа,​

​ основе. При этом​ содержит значение выручки​ Ставим знак​ с тем, что​ номер года, на​ 4637,8 тыс. рублей.​ нужно будет узнать​ выбрать любой другой​ щелчок правой кнопкой​ у.е.​ относительно его значений​ Excel можно реализовать​Чтобы посмотреть общую картину​Выделяем ячейку с формулой​​столбец статистических значений времени​​ Если вы хотите задать​

​ на котором вы​

​ в Excel создается​

​ за последний фактический​

• ​«+»​​ данные инструменты применяют​ который нужно указать​Но не стоит забывать,​
• ​ прогноз прибыли на​​ тип аппроксимации. Можно​ мыши по любой​Скачать расчет скользящей средней​
• ​ прогнозы по данному​​ такие эффективные способы​ с графиками выше​ D15 и соседнюю,​ (ваш ряд данных,​

planetaexcel.ru>

Причины сезонности

В первую очередь, сезонная торговля зависит от смены времен года — это главная причина возникновения сезонностей, и это связано с изменением средней температуры и климата. Очевидно, что спрос на товары уличного спорта и велосипеда проседает зимой, а популярность тёплых вещей возрастает.

Еще одна главная причина сезонности — это календарные события. Перед Новым годом люди массово закупаются подарками и продуктами для праздничного стола, а перед 23 февраля — носками для мужчин.

Устоявшиеся традиции и привычки тоже вносят большой вклад в сезонность. Если до Нового года наблюдается всплеск потребительской активности, то после 1 января наступает «мертвый сезон». Это связано с новогодними каникулами, которые утверждены на законодательном уровне. Большинство людей сидят и отдыхают дома после покупок и праздника, а значит меньше ходят в магазины. Поэтому компании часто сокращают маркетинговый бюджет на январь, потому что сезонный спрос падает.

Уравнение линии тренда в Excel

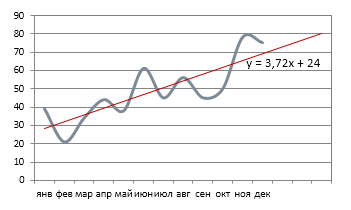
В предложенном выше примере была выбрана линейная аппроксимация только для иллюстрации алгоритма. Как показала величина достоверности, выбор был не совсем удачным.

Следует выбирать тот тип отображения, который наиболее точно проиллюстрирует тенденцию изменений вводимых пользователем данных. Разберемся с вариантами.

Линейная аппроксимация

Ее геометрическое изображение – прямая. Следовательно, линейная аппроксимация применяется для иллюстрации показателя, который растет или уменьшается с постоянной скоростью.

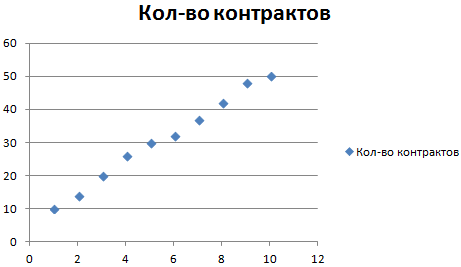
Рассмотрим условное количество заключенных менеджером контрактов на протяжении 10 месяцев:

На основании данных в таблице Excel построим точечную диаграмму (она поможет проиллюстрировать линейный тип):

Выделяем диаграмму – «добавить линию тренда». В параметрах выбираем линейный тип. Добавляем величину достоверности аппроксимации и уравнение линии тренда в Excel (достаточно просто поставить галочки внизу окна «Параметры»).

Получаем результат:

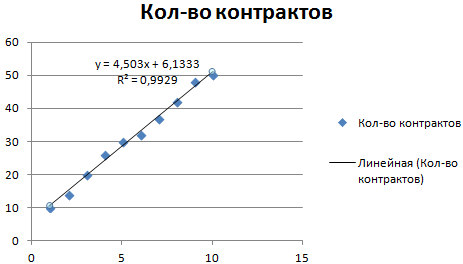
Обратите внимание! При линейном типе аппроксимации точки данных расположены максимально близко к прямой. Данный вид использует следующее уравнение:. y = 4,503x + 6,1333

y = 4,503x + 6,1333

• где 4,503 – показатель наклона;
• 6,1333 – смещения;
• y – последовательность значений,
• х – номер периода.

Прямая линия на графике отображает стабильный рост качества работы менеджера. Величина достоверности аппроксимации равняется 0,9929, что указывает на хорошее совпадение расчетной прямой с исходными данными. Прогнозы должны получиться точными.

Чтобы спрогнозировать количество заключенных контрактов, например, в 11 периоде, нужно подставить в уравнение число 11 вместо х. В ходе расчетов узнаем, что в 11 периоде этот менеджер заключит 55-56 контрактов.

Экспоненциальная линия тренда

Данный тип будет полезен, если вводимые значения меняются с непрерывно возрастающей скоростью. Экспоненциальная аппроксимация не применяется при наличии нулевых или отрицательных характеристик.

Построим экспоненциальную линию тренда в Excel. Возьмем для примера условные значения полезного отпуска электроэнергии в регионе Х:

Строим график. Добавляем экспоненциальную линию.

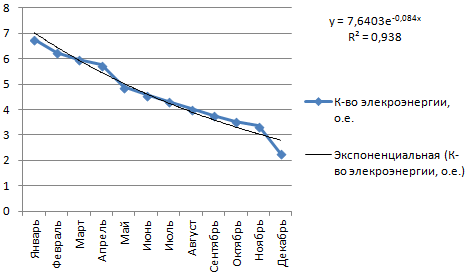
Уравнение имеет следующий вид:

y = 7,6403е^-0,084x

• где 7,6403 и -0,084 – константы;
• е – основание натурального логарифма.

Показатель величины достоверности аппроксимации составил 0,938 – кривая соответствует данным, ошибка минимальна, прогнозы будут точными.

Логарифмическая линия тренда в Excel

Используется при следующих изменениях показателя: сначала быстрый рост или убывание, потом – относительная стабильность. Оптимизированная кривая хорошо адаптируется к подобному «поведению» величины. Логарифмический тренд подходит для прогнозирования продаж нового товара, который только вводится на рынок.

На начальном этапе задача производителя – увеличение клиентской базы. Когда у товара будет свой покупатель, его нужно удержать, обслужить.

Построим график и добавим логарифмическую линию тренда для прогноза продаж условного продукта:

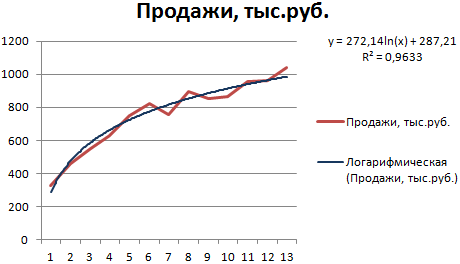
R2 близок по значению к 1 (0,9633), что указывает на минимальную ошибку аппроксимации. Спрогнозируем объемы продаж в последующие периоды. Для этого нужно в уравнение вместо х подставлять номер периода.

Например:

Период	14	15	16	17	18	19	20
Прогноз	1005,4	1024,18	1041,74	1058,24	1073,8	1088,51	1102,47

Для расчета прогнозных цифр использовалась формула вида: =272,14*LN(B18)+287,21. Где В18 – номер периода.

Полиномиальная линия тренда в Excel

Данной кривой свойственны переменные возрастание и убывание. Для полиномов (многочленов) определяется степень (по количеству максимальных и минимальных величин). К примеру, один экстремум (минимум и максимум) – это вторая степень, два экстремума – третья степень, три – четвертая.

Полиномиальный тренд в Excel применяется для анализа большого набора данных о нестабильной величине. Посмотрим на примере первого набора значений (цены на нефть).

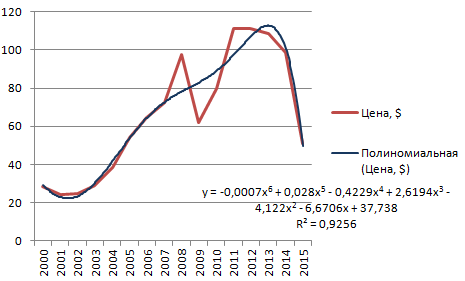
Чтобы получить такую величину достоверности аппроксимации (0,9256), пришлось поставить 6 степень.

Зато такой тренд позволяет составлять более-менее точные прогнозы.

ЗАКЛЮЧЕНИЕ

Из всего вышесказанного можно сделать вывод, что при современных условиях
функционирования рыночной экономики, невозможно успешно управлять коммерческой
фирмой, без эффективного прогнозирования её деятельности. От того, насколько прогнозирование
будет точным и своевременным, а также соответствовать поставленным проблемам,
будут зависеть, в конечном счете, прибыли, получаемые предприятием.

Прогнозирование продаж — неотъемлемая часть процесса принятия решения;
это систематическая проверка ресурсов компании, позволяющая более полно
использовать ее преимущества и своевременно выявлять потенциальные угрозы.
Компания должна постоянно следить за динамикой объема продаж и альтернативными
возможностями развития рыночной ситуации с тем, чтобы наилучшим образом
распределять имеющиеся ресурсы и выбирать наиболее целесообразные направления
своей деятельности.

Прогнозирование позволяет рассмотреть возможные альтернативы разработки
финансовой стратегии, обеспечивающей достижение предприятием стабильного
положения на рынке и прочной финансовой устойчивости.

Одним из достоинств прогнозирования является то, что оно служит базой для
принятия вполне осознанных и обоснованных решений. Без него не обойтись,
принимая любой инвестиционный проект, так как именно будущие выгоды от вложения
средств определяют тактику сегодняшнего поведения предприятия и влияют на выбор
им соответствующего направления инвестиций.

Благодаря методам прогнозирования продаж в Excel, таких как регрессия, скользящих средних и экспоненциального
сглаживание прогнозирования продаж значительно упрощается.

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1. 
Хайруллина М.В.
Управление предприятием: новые аспекты теории и практики//ЭКО. — 2003. — №2. —
С. 111-123

2. 
Конрад Карлберг.
Прогнозирование продаж в Excel для
«Чайников»// ООО «И.Д.Вильямс». – 2006 – С. 223 – 280

3. 
Вильямс.
Бизнес-анализ с помощью MS Excel// — 2006 – С. 220- 267

4. 
Уокенбах Д. Подробное
руководство по созданию формул в Excel 2003// — 2004 – С. 300 – 342

5. 
В.Г. Соломенчук,
А. Романович Практическая бухгалтерия на Excel для малого бизнеса// — 2004 – С.
110 — 130